Общее понятие о состязательных примерах

Виды состязательных примеров

Под атакой на систему машинного обучения в общем виде понимается некоторое преднамеренное вмешательство злоумышленника в процесс ее обучения или инференса. Целью такого вмешательства может являться воспрепятствование ее правильной работе, работа системы таким образом, который желает злоумышленник, кража информации про модель или приватных данных, на которых модель обучалась. Соответственно, обычно выделяют 4 типа атак:

Состязательные атаки (атаки уклонением) - злоумышленник способен воздействовать лишь на вход уже обученной модели - такие атаки мы и будем рассматривать далее. Целью является неверная работа модели.
Атаки отравлением - злоумышленник некоторым образом пытается изменить данные, на которых затем будет обучаться модель. Целью обычно является неверная работа модели (чаще всего работа модели желаемым злоумышленником образом).
Атаки извлечением - злоумышленник по работе модели пытается создать свою локальную копию некоторой модели.
Атаки инверсией - злоумышленник по работе модели пытается восстановить данные, на которых данная модель обучалась.

В рассматриваемых нами атаках уклонением злоумышленник не может ни влиять на обучающие данные, ни каким-либо образом изменять параметры модели. Атакующий может лишь иметь доступ к информации про обученную модель (например, знать ее архитектуру и параметры) или про ее поведение на каких-то входах (то есть наблюдать выходное распределение или присваиваемую изображению метку). Его целью является создать такую ситуацию, когда на вход модели попадет изображение, на котором модель покажет некорректный результат.

Поясним понятие некорректности результата на примере задачи классификации. Именно задаче классификации посвящено большинство статей, посвященных вопросам атак, защит и робастности, хотя эти вопросы будут рассмотрены и для моделей, занимающихся детекцией объектов, семантической сегментацией и другими задачами компьютерного зрения.

Будем обозначать саму нейронную сеть как функцию \(f(x)\), где \(x\) - входное изображение. В случае задачи классификации изображений на \(k\) классов мы имеем функцию \(f: [0,1]^m \rightarrow \{f_1(x), \ldots, f_k(x)\}\), которая принимает на вход нормализованные изображения из \(m\) пикселей, то есть значение каждого пикселя изображения из диапазона \([0, 255]\) приведено к диапазону \([0, 1]\), и возвращает softmax-распределение вероятностей принадлежности к каждому из \(k\) классов: \(\sum_{i=1}^{i=k} f_i(x) = 1, \forall i \: f_i(x) \geq 0\). Результатом классификации является предсказываемый моделью класс, то есть тот, которому она присвоила наибольшую уверенность: \begin{equation} y_{pred} = \underset{i = 1, \ldots, k}{\arg \max} f_i(x) \end{equation}

Пусть имеется изображение \(x^{\prime}\), для которого мы знаем, что оно относится к классу \(y_c\). Под этим мы имеем в виду, что на наш субъективный взгляд или по мнению группы ассесоров данное изображение должно быть отнесено к этому классу. Тогда под некорректной работой модели подразумевается ситуация, когда \(y_{pred} \neq y_c\).

Стоит четко понимать, что модели компьютерного зрения, разумеется, ошибаются и сами по себе, ведь даже для довольного простого датасета MNIST не существуют нейронной сети, которая бы выдавала качество 100% на тестовой выборке (на конец 2022 года лучшая модель показывает качество 99.91%). Под качеством на выборке \(X = \{x^i, y^i\}_{i=1}^{N}\) понимают долю верно классифицированных изображений, то есть: \begin{equation} \sum_{(x^i, y^i \in X)}\mathbb{I} \big[\underset{c = 1, \ldots, k}{\arg \max} \: f_c(x^i) = y^i \big] \end{equation} Еще больше ошибок совершают классификаторы на более сложных и больших наборах данных и в других задачах компьютерного зрения. Однако предметом нашего рассмотрения будут такие ошибки моделей, которые могут быть вызваны злонамеренным вмешательством субъекта в работу некоторой системы машинного обучения. Чаще всего, такое вмешательство приводит к тому, что ошибки, допускаемые в результате состязательных атак, кажутся наблюдателю очень грубыми и контринтуитивными. В отличие от них, ошибки нейронных сетей на обычных изображениях (то есть поступающих на вход без вмешательства человека) зачастую являются более очевидными, например, на вход поступают изображения, которые даже человек не может однозначно отнести к одному классу, или поступают изображения, которые далеки от всех изображений в обучающей выборке. Состязательное изображение, которое должно привести к неверной работе классификатора, может быть выбрано атакующим разными способами. При этом он не всегда даже может контролировать это напрямую. В пособии будут рассмотрены следующие виды состязательных атак:

Нанесение состязательного возмущения - добавление к нормальному изображению \(x\) (например, из тестовой выборки какого-то датасета), которое классифицировалось верно с меткой \(y_c\), небольшого по какой-то норме \(l_p\) шума \(\delta\), такого что \(\underset{i = 1, \ldots, k}{\arg \max} f_i(x+\delta) \neq y_c\), то есть новое изображение классифицируется неверно. Такое возмущение, которое меняет выдаваемый моделью класс, и называется состязательным. Ограниченность состязательного шума по норме имеет целью сделать этот шум незаметным для человеческого глаза, то есть изображение \(x+\delta\) должно выглядеть для человека почти неотличимо от \(x\) и легко классифицироваться человеком с меткой \(y_c\). Именно этому типу атак посвящено большинство статей, где злоумышленник может полностью контролировать вход модели.
Наложение состязательных патчей. Определенный регион изображения (квадратный, круглый или какой-то другой по форме) полностью заменяется на специально подобранный патч (заплатку). Обычно предполагается, что такой патч не закрывает сам классифицируемый объект и для человека по-прежнему понятно, что за предмет находится на изображении. Однако нейронная сеть меняет выдаваемый класс.
Абстрактные состязательные примеры - бессмысленные для человека изображения, (например, выглядящие как белый шум или как какие-то абстрактные паттерны), которые нейронная сеть уверенно относит к классу \(y_i\), то есть для изображения \(x\) \(\exists i\), такой что \(f_i(x) \approx 1\). В отличие от двух предыдущих случаев изображение теперь не содержит объекта ни одного из классов набора данных. Поэтому с нашей точки зрения было бы логично ожидать, что для каждого из \(k\) классов нейронная сеть вернет уверенность \(f_i(x) \approx 1/k\). Следовательно присваивание какому-то из классов близкой к единице уверенности является контринтуитивным и нежелательным поведением.
Физические состязательные примеры - изменение или создание объектов реального мира, которые затем попадают на фото или видеокамеру, а после фотографирования неверно классифицируются нейронной сетью. В качестве примеров такой атаки в физическом мире могут наклеенные на дорожный знак стикеры, надетые на лицо человека очки или даже распечатанный на 3D-принтере объект.

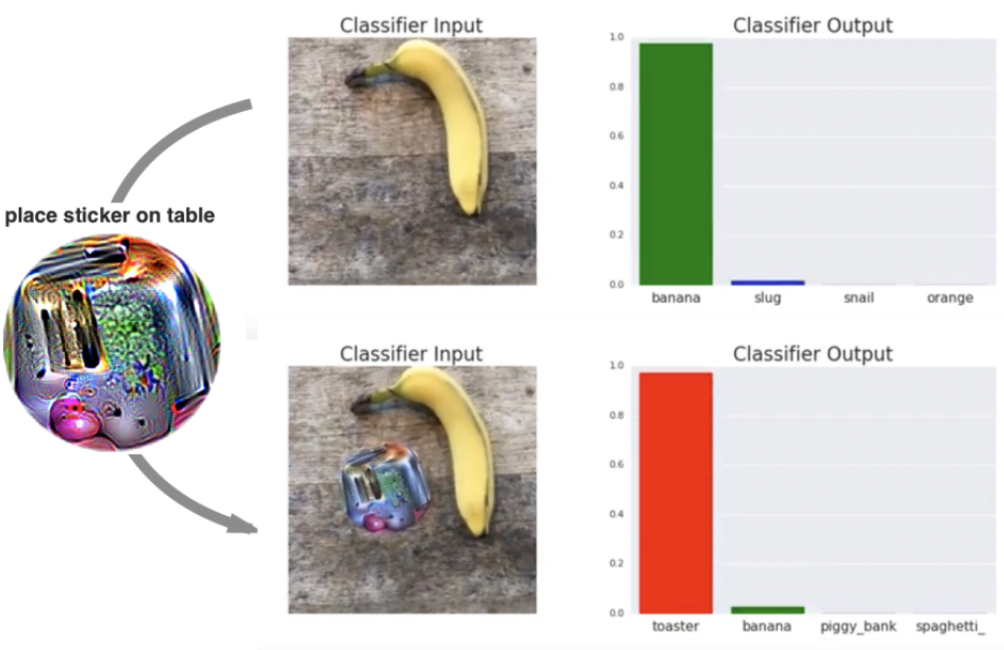
Рис.1 Слева сверху: состязательные примеры для модели AlexNet, обученной на ImageNet. Слева приведены обычные изображения из ImageNet изображения, классифицируемые верно, в центре - вносимый шум, справа состязательные примеры, классифицируемые как страус.Справа сверху: не интерпретируемые изображения, которые нейросеть относит к указанному классу с уверенностью более чем 99.6%. Слева снизу: наложение патча полностью меняет предсказание класса модели VGG-16. Справа снизу: надевание специальных очков приводит к тому, что попавший в камеру человек (сверху), воспринимается нейронной сетью как похожий на совершенно другого человека (снизу).

Классификация состязательных атак

Можно сформулировать обстоятельства и ограничения, при которых злоумышленник будет проводить атаку, и ввести классификацию по различным возможностям злоумышленника. Среди важнейших ограничивающих аспектов атаки можно выделить знания злоумышленника о модели и возможность напрямую контролировать вход модели.

Классификация по знаниям злоумышленника

Атаки в режиме белого ящика (white-box attacks). В этой модели угроз злоумышленник обладает значительной информацией о внутреннем устройстве модели. Чаще всего предполагается знание архитектуры модели и значения всех ее параметров. Это самая сильная модель угроз и она вполне может встречаться в реальной жизни, например в работе "Mind your weight (s): A large-scale study on insufficient machine learning model protection in mobile apps" авторы, не прикладывая значительных усилий, полностью извлекают модели машинного обучения из приложений на мобильных устройствах с операционной системой Android.
Атаки в режиме черного ящика (black-box attacks). В таких атаках не предполагается детального знания об архитектуре и параметрах модели. Однако предполагается взаимодействие с моделью и возможность наблюдать ее выход в зависимости от посылаемого ей входа. Такие атаки можно дополнительно разделить на следующие подкатегории:
Атаки на основе выходного распределения модели. Имеются в виду предсказанные моделью вероятности или логиты (входы на softmax-слой). Во многих случаях суть данных атак сводится к численной оценке градиента (его прямое вычисление невозможно при отсутствии доступа к параметрам модели), в других - используются неградиентные методы оптимизации, например генетические алгоритмы или случайный поиск.
Атаки на основе решения модели. Предполагается наличие доступа только к предсказанному моделью классу объекта.
Атаки на основе переносимости. В самой первой статье по состязательным атакам Intriguing properties of neural networks было открыто, что состязательные примеры могут быть успешно перенесены с одной модели на другую, обученную на том же датасете. В этой модели угроз предполагается наличие доступа или к полному датасету, на котором обучалась целевая модель, или к его части для создания модели-суррогата, для которой и будут синтезироваться состязательные примеры (например, одним из методов белого ящика), а затем эти изображения будут использоваться для атаки на исхожную модель. В некоторых подходах помимо датасета требуется также доступ к выходному распределению модели.

Классификация по контролю над входом модели

Прямой контроль над входом модели. Злоумышленник напрямую определяет пиксели изображения, которые попадут в модель.
Непрямой контроль над входом модели. Злоумышленник не может контролировать пиксели, которые попадут в модель. Чаще всего речь идет об атаках в реальном мире, когда злоумышленник может менять окружающий мир, например наклеивать стикеры, менять внешность и т.п. Целью таких атак является подобрать такие возмущения, которые сохранятся через весь пайплайн данных и будут робастны относительно различных изменений окружающей среды, которые злоумышленник не сможет контролировать.

С другой стороны можно провести ввести классификацию атак по различным свойствам результата атаки. Среди них можно выделить 4 аспекта: цель злоумышленника, универсальности атаки, норме вносимого возмущения, оптимальность/ограниченность вносимого возмущения.

Классификация по цели злоумышленника

Нецелевая атака. Атака считается успешной, если модель присваивает состязательному примеру любой из классов \(y_w\), не совпадающий с правильным классом \(y_c\).
Целевая атака. Атака считается успешной лишь в том случае, если модель присвоила состязательному примеру заранее выбранный определенный неверный класс \(y_{t} \neq y_c\).

Большинство атак имеют и целевую, и нецелевую версию, однако важно понимать, что метрика успешности атака (attack success rate) будет считаться при разных атаках по-разному и, очевидно, что целевая атака всегда будет сложнее, чем нецелевая.

Классификация по универсальности атаки.

Атака для отдельного изображения. Целью атаки является поиск возмущения/патча для отдельного изображения.
Универсальная атака для выборки. Универсальным состязательным возмущением называют такое, которое при наложении на любое изображение из некоторой выборки будет с высокой вероятностью превращать его в состязательный пример (аналогично можно определить и универсальный состязательный патч). Другими словами, значительная доля выборки станет классифицироваться неверно при наложении одного и того же возмущения.

Классификация по норме возмущения.

Когда речь идет о наложении состязательных возмущениях, то чаще всего они предполагаются небольшими и задача атаки формулируется в рамках одной из норм. Пространство изображений одного и того же размера, представленные как вектора \([0, 1]^m\), можно рассматривать как линейное нормированное пространство с нормой \(l_p\).

Выбрав перед атакой одну из норм \(l_p\), злоумышленник затем или ставит задачу поиска состязательного возмущения \(\delta\), ограниченного по норме \(l_p\) сверху каким-то заранее выбранным небольшим значением \(\epsilon\), или ставит задачу оптимизации с целью поиска минимального по норме \(l_p\) состязательного возмущения \(\delta\).

Возмущения по норме \(l_2\). Евклидова норма вносимого возмущения \(\|\delta\|_2 = (\sum_{i=1}^{m} \delta_i^2)^{1/2}\). Эта норма дифференцируема, поэтому ее легко оптимизировать напрямую.
Возмущения по норме \(l_{\infty}\). Максимальное значение возмущения среди всех пикселей: \(\|\delta\|_{\infty} = \underset{i = 1, \ldots, m}{\max}|\delta_i|\). Большинство атак по этой норме ограничивается сверху некоторым \(\epsilon\), и таким образом гарантируется, что значение каждого пикселя изменится не более чем на эту величину.
Возмущения по норме \(l_0\). Норма \(l_0\) вводится специально для изображений и равна количеству ненулевых пикселей вносимого возмущения. Таким образом, если возмущение по норме \(l_0\) равно \(\epsilon\), то мы меняем именно столько пикселей исходного изображения \(x\). При этом диапазон каждого пикселя в возмущении \(\delta\) не ограничен (имеется лишь естественное ограничение, согласно которому состязательный пример \(x+\delta\) должен лежать в диапазоне \([0, 1]^m\)).
Возмущения по норме \(l_1\). \(\|\delta\|_1 = \sum_{i=1}^{m} |\delta_i|\)

Самыми популярными нормами атак являются \(l_2\) и \(l_{\infty}\). Атаки по норме \(l_1\) встречаются довольно редко из-за того, что эта метрика плохо оптимизируется, а также плохо интерпретируема для изображений. Многие атаки имеют версии сразу для нескольких норм.

Классификация по оптимальности.

Минимальное возмущение. Атака проводится с целью найти минимальное по какой-то норме \(l_p\) состязательное возмущение, то есть задача формулируется как \(\underset{\delta}{\arg \max} \|\delta\|_p\) при различных граничных условиях.
Ограниченное возмущение. В такой постановке задачи достаточно найти любое состязательное возмущение, такое что \(\|\delta\|_p < \epsilon\).

Состязательные атаки можно также разделить и по задачам, для которых они создаются, то есть рассматривать атаки на классификаторы, детекторы, сегментаторы и так далее.