Виды защит и их классификация
Наличие состязательных примеров и возможность их синтезировать в режиме черного ящика на основании выходного распределения модели или только лишь используя предсказанный моделью класс, их переносимость с одной модели на другую, а также методы генерации робастных состязательных примеров для физического мира вызвали серьезные вопросы, связанные с безопасностью внедрения моделей компьютерного зрения в реальные системы.
Вместе с развитием техник атак на модели машинного обучения параллельно широко развивалась область защит от состязательных примеров. Однако задача защиты модели от состязательных примеров довольно плохо формализуется.
В самой узкой постановке можно захотеть защитить модель от какой-то конкретной атаки \(A: \mathbb{R}^m \rightarrow \mathbb{R}^m\). Будем считать, что \(A\) переводит исходное изображение \(x\) в некоторое изображение \(x+\delta\), где \(\|\delta\|_p \leq \epsilon\).
Определение Будем говорить, что модель \(f\) с параметрами \(\theta\) имеет робастное качество \(\eta\) относительно атаки \(A\) внутри радиуса \(\epsilon\) на выборке \(X = \{x^j, y_c^j\}_{j=1}^N\) если:
\begin{equation} \frac{1}{N}\sum_{j=1}^{N} \mathbb{I} [\underset{i = 1, \ldots, k}{\arg \max} \; f_i(A(x^j); \theta) = y_c^j] \geq \eta, \end{equation} где \(y_c^j\) -верная метка изображения \(x^j\).
Мы считаем, что радиус робастности \(\epsilon\) небольшой, поэтому для любого \(x^{\prime} \in \mathbb{B}_{\epsilon}(x)\) должна быть верной эта же метка. Это определение имеет лишь эмпирический характер, то есть показывает, что при проведении эксперимента с конкретной атакой \(A\) мы получили конкретное значение. Такое определение довольно слабое. Например, пусть в качестве атаки \(A\) взята атака Iterative-FGSM (PGD). В ней появляется гиперпараметр \(\alpha\) - размер шага на каждой итерации. При одних и тех же \(\epsilon\) и количестве шагов \(T\), но при разных размерах шага \(\alpha\) будут получаться разные \(A(x)\) для конкретного изображения \(x\). Следовательно, и значение определенной метрики будет разным.
С другой стороны можно предложить ввести определение робастности относительно сразу всех существующих атак.
Определение Будем говорить, что модель \(f\) с параметрами \(\theta\) имеет \textbf{робастное качество \(\eta\) } внутри радиуса \(\epsilon\) на выборке \(X = \{x^j, y_c^j\}_{j=1}^N\) если:
\begin{equation} \forall A: \quad \frac{1}{N}\sum_{j=1}^{N} \mathbb{I} [\underset{i = 1, \ldots, k}{\arg \max} \; f_i(A(x^j); \theta) = y_c^j] \geq \eta, \end{equation} где \(y_c^j\) -верная метка изображения \(x^j\).
Под \(A\) в определении подразумевается любая открытая атака. Это определение тоже имеет лишь эмпирический характер. Проблема этой метрики в трудности ее вычисления - необходимо перебрать все открытые атаки. Более того, она не постоянна.
В связи с эим возникает идея все же брать определение робастного качества относительно атаки \(A\), но взять эту атаку очень сильной. В идеале, метрика, даваемая этой атакой, должна быть довольно близка к метрике, получаемой при проведении всего множества открытых атак. В качестве такой атаки был взят ансамбль сильных атак, которые требуют минимальное количество гиперпараметров - Auto-Attack.
Рассмотренные ранее метрики являются лишь только эмпирическими. Можно требовать и математических гарантий того, что внутри сферы \(\mathbb{B}_{\epsilon}(x)\) предсказанный моделью класс не изменится. Такие методы называют * сертификационными*, их можно разделить на 2 категории:
- Формальная верификация - точное доказательство некоторых свойств, например \begin{equation} \forall x^{\prime} \in \mathbb{B}_{\epsilon}(x): \quad \underset{i = 1, \ldots, k}{\arg \max} \; f_i(x^{\prime}; \theta) = \underset{i = 1, \ldots, k}{\arg \max} \; f_i(x; \theta) \end{equation}
- Вероятностная сертификация - приведенное выше свойство выполняется с некоторой вероятностью \(\eta\)
Таким образом, все методы можно разделить на эмпирические и сертификационные. Эмпирические защиты от состязательных атак можно разделить на 3 категории:
- Робастная оптимизация. Методы из этой категории нацелены на повышение эффективности процедуры обучения моделей.
Эту категории можно дополнительно разделить на 3 подкатегории:
- Состязательное обучение. Так как существующие наборы данных не покрывают полностью распределения, на которых классификаторы работают в реальной жизни, а также не включают в себя состязательные примеры, то некоторые техники предлагают синтезировать состязательные примеры прямо во время обучения и подмешивать их к обучающей выборке. Данные методы являются чисто эмпирическими и не предоставляют никаких теоретических гарантий.
- Регуляризация. Эти методы применяют различные техники регуляризации для уменьшения влияния небольших входных возмущений на выход модели.
- Байесовские подходы.
- Усложнение синтеза состязательных примеров (сокрытие/запутывание градиента). Методы из данной категории нацелены на создание моделей, градиенты которых не получится использовать для оптимизации, что помешает выбрать правильное направление для оптимизации. Однако данное методы имеют лишь ограниченную применимость, так как многие атаки (особенно в режиме черного ящика) не используют градиенты.
- Детектирование состязательных примеров. Обучение дополнительных моделей или применение методов из статистики для отделения состязательных примеров от обычных сэмплов.
Каждую из защит принято рассматривать в какой-то из моделей угроз. Обычно выделяют три основные модели угроз (Evasion attacks against machine learning at test time и Adversarial examples are not easily detected: Bypassing ten detection methods):
- Атака с нулевым знанием о защите. Зломышленник синтезирует состязательные примеры с помощью какого-то метода атаки, не задумываясь о возможности защиты модели, и затем защищенная модель оценивается на таких примерах.
- Атаки с полным знанием о защите. Злоумышленник имеет полную информацию о применяемой защите и может провести адаптивную атаку, например изменив функцию потерь в атаке Карлини и Вагнера.
- Атаки с ограниченным знанием о защите. Злоумышленник знает тип защиты, но не знает применяемой в ней параметров.
Такая модель угроз интересна только в том случае, когда атака с нулевым знанием о защите оказалось неуспешной, а атака
с полным знанием о защите - успешной.
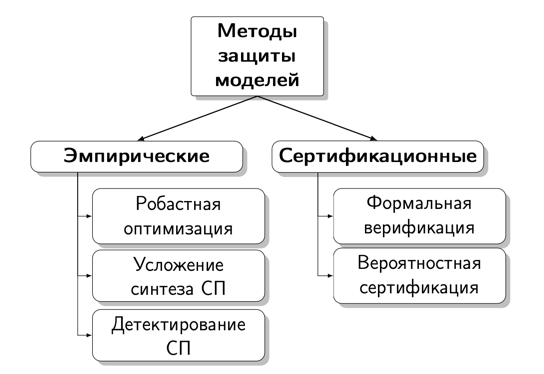
На рис. 1 представлена общая схема методов защит от состязательных примеров.
Робастная оптимизация
Хороший обзор методов робастной оптимизации дан в статье Opportunities and Challenges in Deep Learning Adversarial Robustness: A Survey.
Состязательное обучение
Обычную задачу обучения классификатора с параметрами \(\theta\) на наборе данных \(\mathcal{D}\) с использованием функции потерь \(\mathscr{L}\) можно сформулировать в виде минимизации эмпирического риска на этих данных:
Если же наша задача быть робастными относительно состязательных атак, то есть верно классифицировать состязательные примеры, синтезированные с помощью какой-то атаки, то необходимо модифицировать процедуру обучения.
Пусть определена атака, относительно которой требуется создать робастную модель. Тогда для каждой точки \(x\) из пространства изображений можно установить множество возможный возмущений \(\mathcal{S} \subseteq \mathbb{R}^d\), которые может применить злоумышленник. Чаще всего таким множеством является сфера нормы \(l_p\) вокруг изображения \(x\), где \(p \in \{2, \infty\}\). Тогда в худшем случае злоумышленник внесет возмущение, при котором функция потерь достигнет максимума на множестве \(\mathcal{S}\). Следовательно, для рассматриваемой атаки задачу обучения можно сформулировать как задачу седловой точки:
Задача внутренней максимизации является высоко размерной невыпуклой задачей, которую очень сложно решить существующими методами оптимизации. Поэтому в большинстве подходов предлагается решать ее приблизительно. Из-за этого данные подходы являются эмпирическими и не дают теоретических гарантий. Но, в отличие от методов сертификационной защиты, методы состязательного обучения обычно демонстрируют значительно более высокие метрики.
Состязательное обучение с FGSM сэмплами
Первыми предложили использовать состязательные примеры во время обучения Goodfellow et al. в работе EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES. Они использовали FGSM для синтеза состязательных примеров и смешивали их с примерами из обучающей выборки.
Такой подход позволил сократить уровень ошибки с \(89.4\%\) до \(17.9\%\) на состязательных примерах, полученных с помощью FGSM. Состязательные примеры, полученные с помощью модели, обученной таким образом, оказались более робастными: при переносе их на оригинальную модель уровень ошибки составил \(40.9\%\), в то время как перенос состязательных примеров с оригинальной модели на новую привел к уровню ошибки \(19.6\%\).
Kurakin et al. в работе также предложили обучать модели состязательно на примерах, полученных методом FGSM, однако использовать его целевую версию FGSM-LL, где в качестве целевого лейбла берется наименее вероятный, то есть такой, для которого модель на чистом сэмпле выдает наименьшую вероятность \(y_{LL} = \underset{y}{\arg \min} \{p(y|X)\}\). Каждый батч для обучения по идее авторов состоит наполовину из чистых сэмплов, а наполовину - из состязательных. Значение функции потерь на батче авторы вычисляют по следующей формуле:
Однако данный подход с состязательным обучением на FGSM-сэмплах на самом деле является очень ограниченным, так как не защищает против более сложных атак. В работе Ensemble adversarial training: Attacks and defenses было также показано, что данная методика неэффективна против атак в режиме черного ящика (перенос с других моделей), а также даже против одношаговых атак, если использовать сэмплы полученные с помощью R-FGSM. Так, если для обученной состязательно Inception v3 уровень ошибки на FGSM-LL-сэмплах составил \(26.6\%\), то на R-FGSM-LL-сэмплах уровень ошибки увеличился до \(64.8\%\).
Были проанализированы причины такого поведения. Если мы аппроксимируем в в задаче седловой точки внутреннюю задачу максимизации методом FGSM, то у нас могут получиться 2 различных случая:
- Для точки \(x\) из пространства изображений \(\mathcal{D}\) и модели с параметрами \(\theta\) не существует состязательного примера \(x^{adv}\), близкого к \(x\) по норме \(l_{\infty}\), который бы приводил к высокому значению функции потерь, то есть:
- Для модели с параметрами \(\theta\) метод FGSM вблизи точки \(x\) из пространства изображений \(\mathcal{D}\) плохо аппроксимирует поведение ее функции потерь и синтезируют состязательные примеры, которые далеки от оптимальных ( вырожденный минимум):
Авторы установили, что в случае вырожденного минимума не производится общего повышения робастности модели. На самом деле FGSM, примененная к модели, обученной таким образом, лишь синтезирует более слабые состязательные примеры, которые могут быть легко классифицированы даже незащищенной моделью. Этот тезис был подтвержден экспериментально.
Введем понятие \textit{уровень аппроксимации(approximation-ratio)} метода FGSM-LL для модели с параметрами \(\theta\) на наборе данных \(\mathcal{D}\). Оно имеет смысл того, насколько хорошо FGSM-LL приближает значение функции потерь относительно самого сильного состязательного примера: \begin{equation} \text{approximation-ratio} = \underset{x \in \mathcal{D}}{\mathbb{E}} \; \Bigg[\frac{\mathscr{L}(\theta, x+\delta^{adv}{FGSM}, y{true})} {\underset{\delta \in \mathcal{S}}{\max} \, \mathscr{L}(\theta, x + \delta, y_{true})} \Bigg] \end{equation}
Так как мы не можем точно вычислить знаменатель, то мы аппроксимируем его более мощными итеративными атаками PGD, тем самым рассматриваем верхнюю границу уровня аппроксимации. Для \(1,000\) сэмплов из ImageNet на обычной модели Inception v3 значение approximation-ratio получилось равным \(0.19\). Для состязательно обученной Inception v3 уровень аппроксимации снижается до \(0.07\), тем самым показывается, что состязательно обученные модели хуже поддаются линеаризации.
К аналогичным выводам можно придти, рассчитав cosine similarity между FGSM-LL-сэмплами и PGD-сэмплами. Чем более линейна модель, тем больше эти величина должна быть. Для Inception v3 средняя величина cosine similarity составила \(0.13\), а для состязательно обученной ее версии - лишь \(0.02\) https://arxiv.org/pdf/2001.03994.pdf.
Защита Madry
Madry et al. в работе Towards Deep Learning Models Resistant to Adversarial Attacks для решения задачи поиска седловых точек предложили аппроксимировать внутреннюю задачу максимизации с помощью PGD, называя его универсальной атакой среди методов первого уровня (на основе градиента).
| Параметр | Значение |
| Статья | https://arxiv.org/pdf/1706.06083.pdf |
| Код | MNIST, CIFAR-10 |
| Норма | l∞ |
| Задача | Классификация |
| Модели | LeNet, ResNet |
| Наборы данных | MNIST, CIFAR-10 |
| Состояние | ϵ = 0.3 : 88%, MNIST |
Во-первых, авторы провели эксперимент, в котором запускали PGD много раз (\(10^5\)) с разными инициализациями. Оказалось, что во всех случаях значение функции потерь увеличивается и выходит на плато, то есть наблюдается сходимость. Так же оказалось, что итоговые значения функции потерь оказываются очень близки к другу и выбросов не наблюдается, то есть при разной инициализации мы будем приходить к разным точкам, но их значения будут близки. На основании этого авторы утверждают, что методы, также использующие лишь градиент для синтеза состязательных примеров, не смогут найти точку с сильно лучшим значением функции потерь (такая может существовать, но ее вычислительно сложно найти). Авторы иллюстрируют данное утверждение экспериментами.
Для решения общей задачи авторы сначала решают внутреннюю задачу максимизации с помощью PGD, а затем подставляют это значение во внешнюю задачу и решают ее с помощью SGD (на основе теоремы Данскина). Авторы показывают эффективность своей защиты против атак в норме \(l_{\infty}\) на наборах данных MNIST и CIFAR-10. \
На датасете MNIST модель LeNet была обучена на состязательных примерах, полученных методом PGD при \(\epsilon=0.3\). Состязательные примеры в режиме белого ящика на валидации синтезировались с таким же \(\epsilon\) атаками FGSM, PGD с разным количеством итераций и рестартов, CW, а также ее версию CW+ с параметром \(k=50\). Также исследовалась робастность относительно перенесенных с других моделей состязательных примеров (модель \(A^{\prime}\) имеет такую же архитектуру и обучалась независимо, модель \(B\) имеет другую архитектуру из статьи The Space of Transferable Adversarial Examples). В качестве метрики использовалась accuracy.