Основы математического анализа
Предел, производная, дифференциал. Производная по направлению, градиент. Первообразная, интеграл. Производные высших порядков, максимум и минимум поверхности, ряд Тейлора.
Основная идея или метод решения задач в математическом анализе состоит в замене функций, с которыми тяжело работать, на близкие к ним (с устраивающей нас разницей/погрешностью приближения), которые уже давно изучены и понятны, то есть с которыми работать легко. В жизненных задачах как правило нам не нужно знать само точное значение, а достаточно понимать порядок (количество цифр в записи числа) или приближение с нужной нам точностью.
Приведём пример с покупкой квартиры: предположим, что она стоит 9 987 567 рублей, но нам легче округлить до 10 миллионов, поскольку это проще и понятнее воспринимается. Но есть тонкий момент: 8 987 567 мы тоже можем округлить до 10 миллионов, только порядок округления может не всех устроить. В первом случае мы прибавили около 100 000, что составляет 0,01 от исходной цифры, а во втором случае - около 1 100 000, что составит уже 0,1 от исходной цифры, а такое приближение уже не все могут себе позволить.
Лучше идеи с переходом к окрестности точки ещё никто не смог придумать, логика такова: надо определить понятие максимально близких точек, то есть расстояние между которыми очень близко к нулю, или другими словами, они находятся в одном интервале, длина которого очень маленькая. В терминах математики: \(\epsilon\)-окрестность точки \(x_0\) - интервал \((x_0-\epsilon;x_0+\epsilon)\), где \(\epsilon\) - очень маленькое число. А дальше заменяем значение функции в точке на значения функции в точках, максимально близких к рассматриваемой, или из той же окрестности.

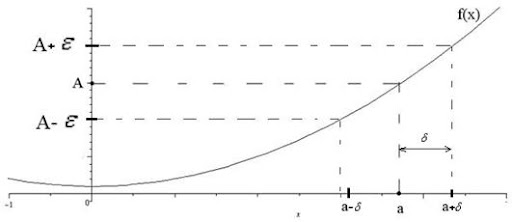
Строгое определение: число \(A\) называется пределом функции \(f(x)\) при \(x\) стремящемся к \(a\), если для любого, сколь угодно малого положительного числа \(\epsilon\) найдётся такое положительное число \(\delta\), что для любого \(x\) из проколотой \(\delta\)-окрестности точки \(a\) значения функции\(f(x)\) попадают в \(\epsilon\)-окрестность f(a)=A:
\(0<|x-a|<\delta \Rightarrow |f(x) -A|<\epsilon.\)
Итак, точки мы заменяли на близкие им точки, а функции будем заменять на близкие им функции. Напомним определение: функция - правило, по которому одному числу из множества \(X\) ставится в соответствие одно число из множества \(Y\). Функция может быть задана: таблицей, графиком, формулой, алгоритмом. Чаще всего мы работаем с формулами и графиками. Теперь у нас стоит задача: понять, где функция растёт, где убывает, в каких точках достигает максимальное и минимальное значения. Если у нас есть график, то всё просто видно, а вот если функция задана формулой, причём довольно сложной, нужно придумывать обходные пути.
Для начала определимся, как понимать рост функции \(y=f(x)\): если при увеличении \(x\) увеличивается \(y\), то функция возрастает, если наоборот, при увеличении \(x\) уменьшается \(y\), то функция убывает. Теперь определим как именно функция возрастает, то есть с какой скоростью. Из физики мы помним, что скорость - это искусственно введённая величина, которая показывает какую часть расстояния мы преодолели за единицу времени. В терминах нашей задачи нас интересует мгновенная скорость: как изменился \(y\) при небольшом изменении \(x\). То есть мы совсем немного увеличили \(x\) (существуем в \(\epsilon\)-окрестности), и смотрим, как изменится \(y\). В качестве примера возьмём всё ту же гиперболу \(y=\frac{1}{x}\): при одном и том же изменении \(\Delta x=0,0009\) с \(0,0001\) до \(0,001\) \(y\) изменился на 900 единиц, а при изменении с \(100,0001\) до \(100,001\) всего на \(0,00000009\) - разница внушительная.
Итак, зафиксируем точку \((x;y)\) и переместимся во вторую точку \((x+\Delta x;y+ \Delta y)\), скорость роста тогда равна \(\frac{\Delta y}{\Delta x}\). Осталось вспомнить, что мы работаем с близкими точками, когда \(\Delta x\) очень мала, по сути точки \((x;y)\) и \((x+\Delta x;y+ \Delta y)\) почти сливаются и соединяющая их прямая превращается в касательную, проходящую через эти слипшиеся точки. Осталось воспользоваться понятием предела и получить итоговое определение:
Производной функции \(f(x)\) называется новая функция \(f'(x)\), которая показывает скорость роста исходной функции в окрестности данной точки:
\(f'(x) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}\)
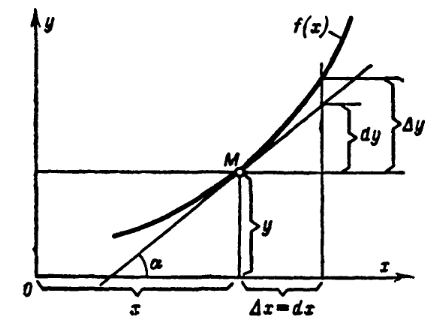
Геометрически получается, что это отношение как раз есть тангенс угла наклона касательной \(f'(x)= \tan{\alpha}\). Другими словами, мы приближаем нашу функцию касательной, проходящей через точку \((x;y)\), потому что поведение касательной однозначно может сказать, что происходит с функцией: касательная идёт вверх \(\tan{\alpha}>0\) - функция возрастает, касательная идёт вниз \(\tan{\alpha}<0\) - функция убывает. Идея поиска максимума и минимума, известная со школы - найти нули производной (таблицу производных для нас уже давно посчитали учёные) и точки, в которых функция определена, а производная - нет. Далее выбираем те точки, в которых производная меняет знак.
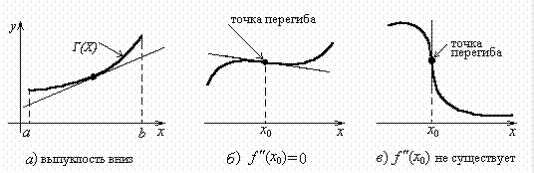
Если первая производная - это скорость роста функции или тангенс угла наклона касательной к графику функции, то вторая производная - ускорение, или скорость роста тангенса угла наклона касательной. Получается, что если тангенс растет, то касательная огибает график, заворачиваясь влево, если тангенс убывает, то касательная заворачивается вправо. Вторая производная позволяет находить точки перегиба: в самой точке первая производная \(f'(x_0)\) равна нулю или не существует, но слева и справа от точки перегиба вторая производная \(f''(x_0)\) имеет разные знаки:
Теперь посмотрим на график и заметим, что при замене функции касательной, расстояние \(\Delta y\) изменилось на \(dy\) и скорость \(\frac{\Delta y}{\Delta x}\) изменилась на мгновенную скорость \(\frac{dy}{dx}\), отсюда следует определение дифференциала - приращение ординаты касательной к графику функции: \(dy = f'(x) \Delta x = f'(x) dx\), так как \(\Delta x = dx\) из построения функции \(y=x\). Физический смысл дифференциала: если бы тело сохранило набранную скорость \(f'(x)\), то через время \(dx\) проехало расстояние \(dy\). Другими словами, в физической задаче мы заменим движение с ускорением на равномерное движение и будем искать пройденный путь через эту постоянную скорость. Производную можно рассматривать как отношение дифференциалов функции и её аргумента.
Скоцентрируем внимание на различии: \(\Delta y\) - на сколько изменилась сама функция \(f(x)\) при изменении аргумента на \(\Delta x\), \(dy\) - на сколько изменилась касательная к функции при изменении аргумента на \(\Delta x\).
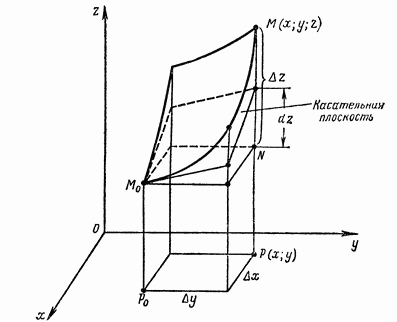
В трёхмерном случае касательная линия заменяется на касательную плоскость и дифференциал показывает приращение аппликаты касательной плоскости. Самым общим случаем замены функции в окрестности точки является Ряд Тейлора - по сути приближение с нужной точностью \(R\) в заданной окресности точки \(a\) любой функции \(f(x)\) степенными функциями с соответствующим весом - скоростью роста или производной - сначала линейной с весом скорости, потом параболой с весом ускорением и так далее.
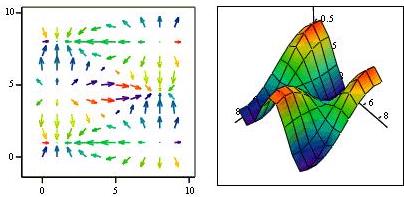
Новые задачи: есть холм, нам надо максимально быстро взобраться на него, а так же изобразить трёхмерную фигуру на плоскости. Обе эти задачи помогает решить градиент. Начнём с рисунка ниже.
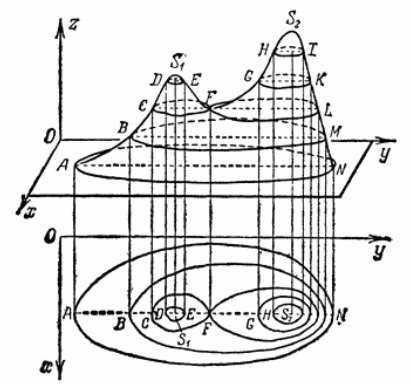
Первая мысль - сделать срезы через равные промежутки по высоте. Такие срезы называются линями уровня, то есть кривые, на которых функция принимает одно и то же значение \(f(x,y) = const\). Но возникает проблема - на такой картинке один и тот же холм по форме, но выпуклый или вогнутый, визуально будет выглядеть одинаково. Разумно ввести направление вверх или вниз. Возьмём точку и посмотрим поведение заданной функции в данной точке. Для этого направим во все стороны векторы из этой точки и посмотрим как изменяется функция вдоль направления каждого вектора \(\vec l\). Вспоминаем, что за скорость роста отвечает производная, то есть создадим векторное поле с весами \(\{ f'_x, f'_y \}\), которые будем скалярно умножать на выбранное направление \(\vec l\) или в терминах проекций \(l=(\cos \alpha, \cos \beta)\):
\(\{ f'_x, f'_y \} \cdot \vec l = f'_x \cos \alpha + f'_y \cos \beta\)
Заметим, что данное выражение максимально, когда \(\cos \alpha =1, \cos \beta = 1\), то есть выбранное направление совпадает с направлением вектора \((f'_x, f'_y)\). Итак, одна из интерпретаций градиента (обозначение \(grad f\))- это правило, по которому мы строим векторное поле с весами \(\{ f'_x, f'_y \}\) или правило, которое таким способом переводит скалярное поле в векторное.
Производную по направлению можно также рассматривать как скалярное произведение градиента и заданного направления \((grad f, \vec l)\). Ещё можно встретить интерпретацию градиента, как вектора, указывающего направление наискорейшего роста функции. Отметим, что в каждой точке свой вектор-градиент, его началом будет эта точка, а направление совпадает с направлением наискорейшего роста функции, модуль вектора-градиента показывает скорость изменения функции в заданной точке.
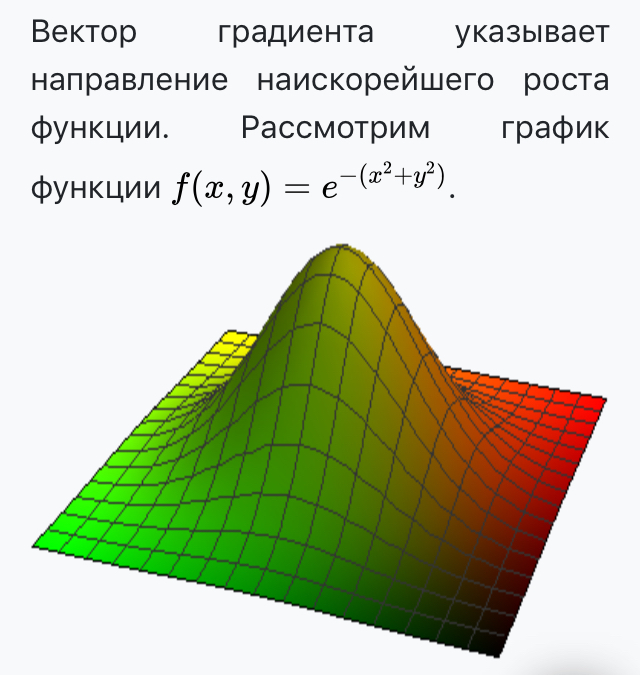
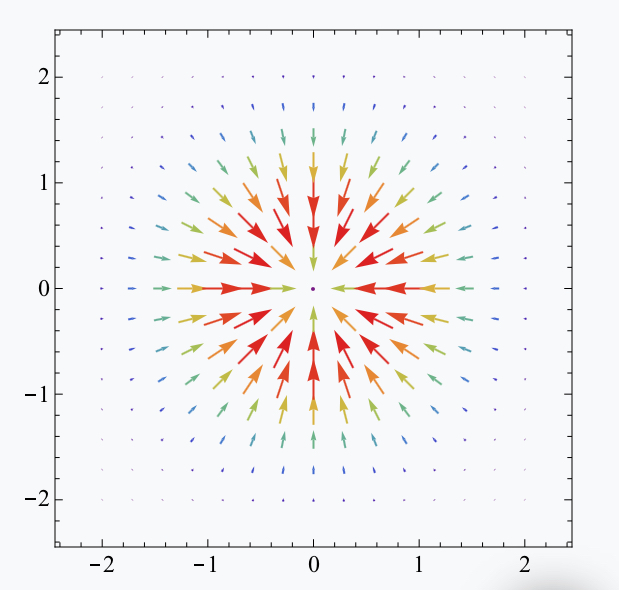
Итого для изображения трёхмерных поверхностей на плоскости вводим вектор-градиент, который покажет направление роста, а также цветовую шкалу синий - минимальные значения (показатель глубины), красный - максимальные (показатель высоты). Представленные таким образом поверхности выглядят уже хорошей интерпретацией:
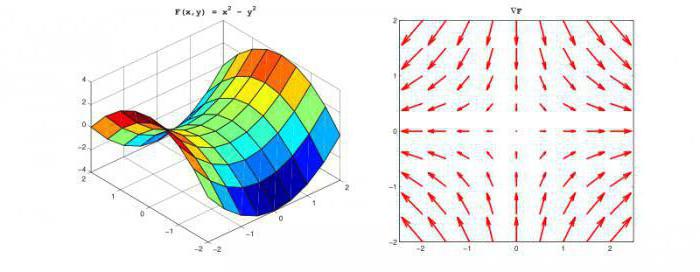
Разберёмся с градиентом в более строгой математической форме: итак, нам надо понять, как описать рост поверхности, заданной уравнением \(z= f(x,y)\). Вспомним, что рост мы определяем через значение приращения и производную:
\(f(x+\delta x) - f(x) = f'_x \delta x + o(\delta x) = f'_x \,dx + o(dx)\)
\(f(y+\delta y) - f(y) = f'_y \delta y + o(\delta y) = f'_y \,dy + o(dy)\)
То есть рост функции \(z=f(x,y)\) можно определить как суммарный рост вдоль осей \(Ox\) и \(Oy\). Фиксируем точку на поверхности, откладываем от неё два вектора, параллельные \(dx\) и \(dy\), они задают плоскость, а сдвиг вдоль этой плоскости будет равен \(dz = f'_x dx + f'_y dy\). В терминах скалярного произведения градиент - это функция от вектора, равная скалярному произведению \((f'_x,f'_y)(dx,dy)\). Ещё раз отметим, что вектор-градиент лежит в плоскости векторов \((dx,dy)\). Смысл градиента любой скалярной функции \(f\) в том, что его скалярное произведение с бесконечно малым вектором перемещения \(dx\) даёт полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена \(f\), то есть линейную (в случае общего положения она же главная) часть изменения \(f\) при смещении на \(dx\).
Модуль градиента показывает максимальную скорость изменения функции в окрестности, то есть частоту линий уровня. Например, линии уровня высоты изображаются на топографических картах, при этом модуль градиента показывает крутизну спуска или подъёма в данной точке.
\(|grad \phi | = \sqrt{ \Biggl( \frac{\partial \phi}{\partial x} \Biggr)^2+ \Biggl( \frac{\partial \phi}{\partial y} \Biggr)^2 + \Biggl( \frac{\partial \phi}{\partial z} \Biggr)^2}\)
Градиент - вектор, направленный по нормали к поверхности уровня в сторону наибольшего возрастания функции и по модулю равный скорости изменения функции.
Теперь разберёмся с производными второго порядка:
\(f''_{xx}, \, f''_{xy}, \, f''_{yy}\).
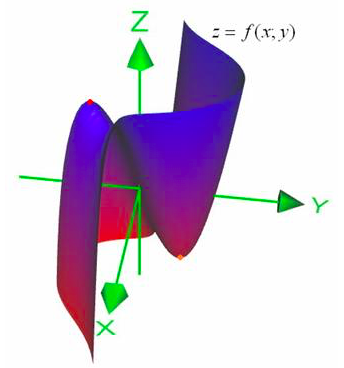
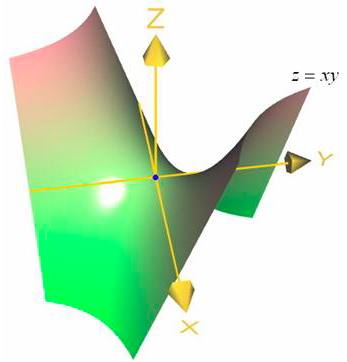
Надо понять, как искать максимум и минимум функции, заданной в трёхмерном пространстве \(z=f(x,y)\). Сначала заметим, что в точках экстремума первые производные \(f'_x, \,f'_y\) либо равны нулю, либо не существуют, так как при проекциях на плоскости \(0zx\) и \(0zy\) точки экстремума остаются точками экстремума. Решаем систему уравнений \(f'_x=0, \, f'_y =0\) и находим точки-кандидаты на экстремумы. В окрестностях этих точек приблизим данную поверхность по формуле Тейлора до второго порядка:
\(z-z_0 = dz + d^2z + \,R = f'_x dx \,+\, f'_y dy \,+\, f''_{xx} (dx)^2 \,+\, 2f''_{xy} dx dy \,+\, f''_{yy} (dy)^2 \,+\, R\)
\(= f''_{xx} (dx)^2 \,+\,\, 2f''_{xy} dx dy \,+\, f''_{yy} (dy)^2 \,+\, R\)
\(z > z_0\), если полученная квадратичная форма положительно определена, \(z < z_0\) - если отрицательно. За это отвечает критерий Сильвестра:
\(\Delta = det \begin{bmatrix} f''_{xx} & f''_{xy} \\ f''_{xy} & f''_{yy} \end{bmatrix}\)
1) если \(f''_{xx} > 0\) и \(\Delta >0\), то в точке будет минимум;
2) если \(f''_{xx} < 0\) и \(\Delta >0\), то в точке будет максимум;
3) если \(\Delta <0\), то экстремума не будет;
4) если \(\Delta = 0\), то возникает неопределённость, надо продолжать исследования через производные третьего порядка и т.д.
Обобщением на \(n-\)мерный случай для вектор-функции \(f=(f_1, \dots, f_n)\) служат две матрицы и их определители:
Якобиан отвечает за линейное приближение касательной плоскостью, определитель матрицы первых частных производных:
\(J_f (x) = det \begin{bmatrix} \frac{\partial f_1(x)}{\partial x_1} & \dots & \frac{\partial f_1 (x)}{\partial x_n} \\ \dots & \dots & \dots \\ \frac{\partial f_n (x)}{\partial x_1} & \dots & \frac{\partial f_n (x)}{\partial x_n} \end{bmatrix}\)
Гессиан отвечает за обобщённую локальную кривизну - приближение квадратичной формой, определитель матрицы вторых частных производных:
\(H_f (x) = det \begin{bmatrix} \frac{\partial^2 f(x)}{\partial x_1^2} & \dots & \frac{\partial^2 f (x)}{\partial x_1 \partial x_n} \\ \dots & \dots & \dots \\ \frac{\partial^2 f(x)}{\partial x_n \partial x_1} & \dots & \frac{\partial^2 f (x)}{\partial x_n^2} \end{bmatrix}\)
Метод множителей Лагранжа. Метод Каруша-Кунна-Таккера.
Под условным экстремумом понимают максимальное или минимальное значение функции \(f\) в области, ограниченной какими-либо условиями, например \(\phi_i = 0\) или \(\phi_i \le 0\).
Рассмотрим поверхность вращения \(z = f(x,y)\) в трёхмерном пространстве, и её сечение поверхностью \(\phi (x,y) = 0\). Данное сечение будет плоской кривой, например, параболой или эллипсом, понятно, что нижняя точка их пересечения - минимум \(f\) при заданных условиях, верхняя - максимум \(f\).
Вспомним про линии уровня: если спроецировать картинку на плоскость \(0xy\), то получим линии уровня и кандидат на экстремум - точка, в которой пересекаются касательная к линии уровня и касательная к параболе.
Таким образом задача сводится к отысканию такой точки линии уровня, в которой функция принимает экстремальное значение, причем сравниваются значения функции только в точках рассматриваемой линии. Надо понять, как находить эти точки максимума и минимума аналитически.
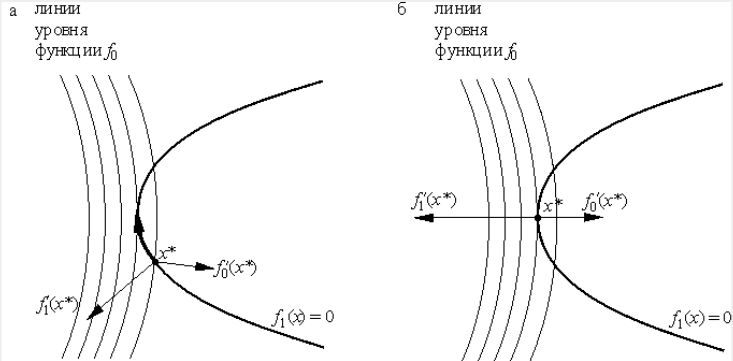
Так как обе функции пересекаются в одной точке, то касательная, проходящая через эту точку, общая для обеих функций. Вспомним также, что градиент показывает направление наискорейшего роста функции, а также перпендикулярен к линиям уровня и к касательным, проходящим через указанную точку.
Получаем важный факт: \(grad \,f\) и \(grad \, \phi\) лежат на одной линии, то есть пропорциональны или \(grad f = \lambda \, grad \, \phi\), получаем систему уравнений
\(\frac{\partial f}{\partial x} (x_0) = \lambda \frac{\partial \phi}{\partial x} (x_0),\)
\(\frac{\partial f}{\partial y} (y_0) = \lambda \frac{\partial \phi}{\partial y} (y_0),\)
\(\phi(x_0,y_0) = 0\)
Лагранж вводит новую функцию \(L(x,\lambda) = f(x) + \sum_i \lambda_i \phi_i\), которая по сути является такой сдвинутой функцией \(f(x)\), что безусловный экстремум \(L\) совпадает с условным экстремумом \(f\), и частные производные функции \(L\) по \(x_i\) и \(\lambda_i\) задают уравнения для поиска условного экстремума функции \(f\):
\(\frac{\partial f}{\partial x}\Big|_{(x_0,\;y_0)} +\lambda_0 \cdot \frac{\partial\phi}{\partial x}\Big|_{(x_0,\;y_0)} = 0, \phi(x_0, y_0)\)
\(\frac{\partial f}{\partial y}\Big|_{(x_0,\;y_0)} +\lambda_0 \cdot \frac{\partial\phi}{\partial y}\Big|_{(x_0, y_0)} = 0, 0.\)
Обобщением метода множителей Лагранжа на случай ограничений в виде неравенств называется Метод Каруша-Куна-Таккера и заключается в следующем: надо найти многомерную величину с неотрицательными компонентами \(x=(x_1, \dots, x_n)\), которая будет точкой минимума функции \(f(x)\) с ограничениями \(g_i(x) \le 0, \, i=1,\dots, n\). Вводим функцию Лагранжа \(L(x,\lambda) = f(x) + \sum \lambda_i g_i(x)\), и чтобы \(\hat x\) была точкой минимума, должны выполняться следующие условия:
-
\(\hat x\) - точка минимума функции \(L\)\
-
условия не жёсткости \(\lambda_i g_i (\hat x) =0\)\
-
\(\lambda_i \ge 0\)
Метод наименьших квадратов. Метод градиентного спуска.
Как мы уже говорили, основная идея большинства изучаемых нами математических методов сводится приближению или замене сложных для понимания исследуемых функций на более простые и уже изученные с заданной точностью. Самым явным примером применения этой идеи является метод наименьших квадратов, которым активно пользуются физики и экономисты. Сразу оговорим, что под наименьшими квадратамиподразумевается минимизации суммы квадратов погрешностей приближения.
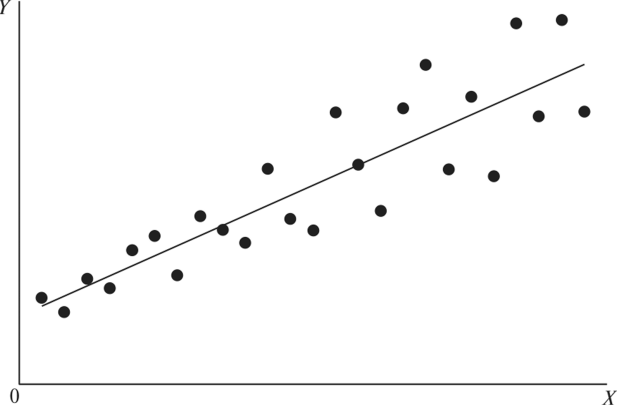
Есть серия данных, полученных во время опыта, их можно записать в виде таблицы и изобразить на графике. Если точки на графике группируются вокруг прямой \(\hat y=ax+b\), то можно подобрать коэффициенты при помощи вычислений.
Если \((x_i,y_i)\) - полученные данные, а \(\hat y_i\) - теоретические значения ординаты, тогда определим погрешности вычисления как \(\epsilon_i = \hat y_i - y_i = ax_i+b-y_i\). Наша задача: подобрать коэффициенты \(a\) и \(b\) так, чтобы сумма погрешностей \(|\epsilon_i|\) была наименьшей. Составим функцию \(e=\sum_i \epsilon_i^2\) и будем минимизировать её, поскольку при наименьших возможных \(\epsilon_i^2\) будут наименьшими \(|\epsilon_i|\):
\(e=\sum_i \epsilon_i^2 = \sum_i ( ax_i+b-y_i )^2, \quad \frac{\partial e}{\partial a} = 0, \quad \frac{\partial e}{\partial b} = 0\)
\(\frac{\partial e}{\partial a} = 2 \sum_i ( ax_i+b-y_i ) x_i = 2a \sum_i x_i^2 + 2b \sum_i x_i - 2 \sum_i x_i y_i = 0\)
\(\frac{\partial e}{\partial b} = 2 \sum_i ( ax_i+b-y_i ) = 2a \sum_i x_i + 2bn - 2 \sum_i y_i = 0\)
Получаем систему для нахождения коэффициентов \(a\) и \(b\) через известные \((x_i,y_i)\):
\(a \sum_i x_i^2 + b \sum_i x_i = \sum_i x_i y_i\)
\(a \sum_i x_i + bn = \sum_i y_i\)
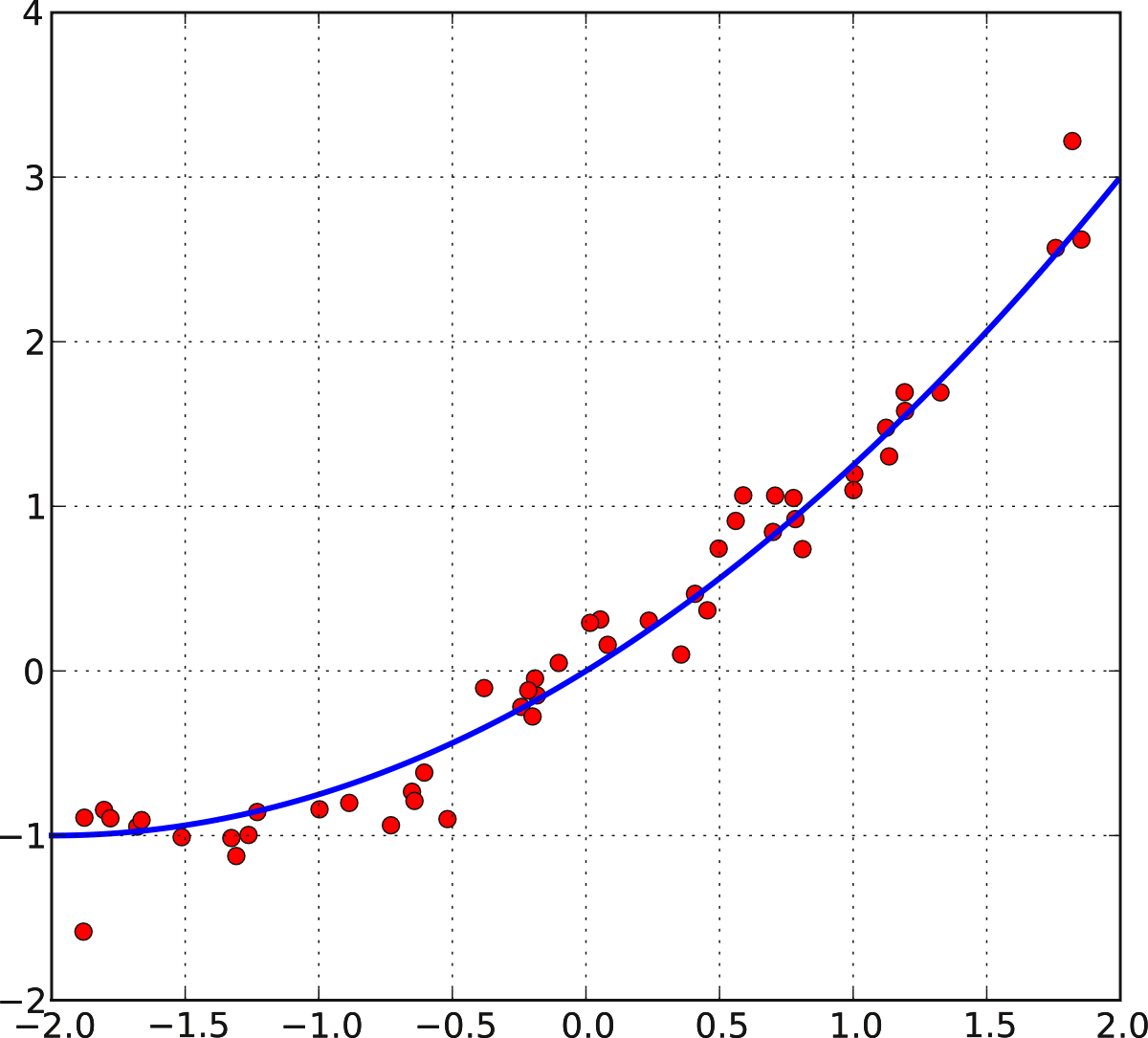
Аналогичным образом получаем систему уравнений для нахождения коэффициентов при приближении параболой \(\hat y = ax^2+bx+c\)
\(a \sum_i x_i^4 + b \sum_i x_i^3 + c \sum_i x_i^2 = \sum_i x_i^2 y_i\)
\(a \sum_i x_i^3 + b \sum_i x_i^2 + c \sum_i x_i = \sum_i x_i y_i\)
\(a \sum_i x_i^2 + b \sum_i x_i + cn = \sum_i y_i\)
Метод градиентного спуска - алгоритм для нахождения минимума функции \(f\). Как мы уже обсуждали, градиент задаёт направление наискорейшего подъёма, соответственно, двигаясь в противоположном направлении, будем максимально быстро спускаться.
Идея следующая: выбираем стартовую точку \(x_0\) и спускаемся вниз, вдоль направления, противоположного градиенту, с заранее заданной длиной шага \(h\), в точку \(x_1\). Другими словами, вектор \(-\frac{\partial f}{\partial x_k^i}\) растягиваем в \(h\) раз, его начало помещаем в точку \(x_0\), а его концом будет точка \(x_1\). На каждом шаге проверяем, уменьшилось ли значение функции и насколько. Если значение функции уменьшается больше заданной точности \(\epsilon\), то берём точку \(x_1\) за исходную и повторяем процесс, пока значения на последующем шаге будет мало отличаться от значения на предыдущем шаге:
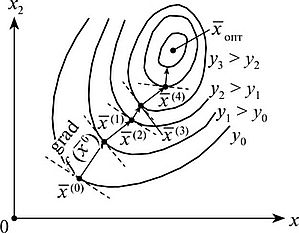
\(x_k^{i+1} = x_k^i - h \frac{\partial f}{\partial x_k^i}\)
За меру близости к минимуму удобно принять сумму абсолютных значений производных
\(\epsilon = \sum_i \Bigl| \frac{\partial f}{\partial x_k} \Bigr|\)
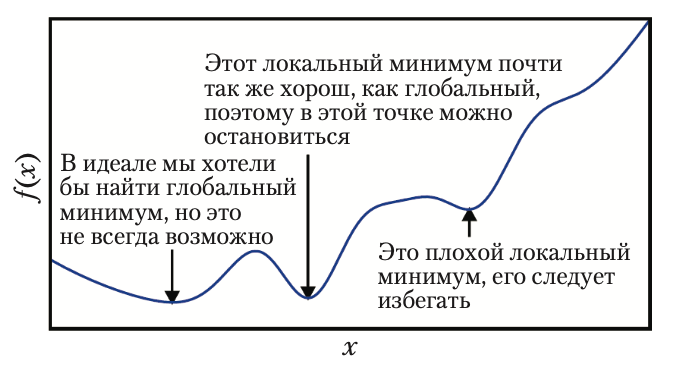
Есть проблема выбора длины шага \(h\): если он будет очень мал (точный поиск), мы будем двигаться слишком медленно и процесс займёт слишком много времени, а если \(h\) будет слишком большим (грубый поиск), мы рискуем перескочить через минимум и попасть в другую яму, менее глубокую.
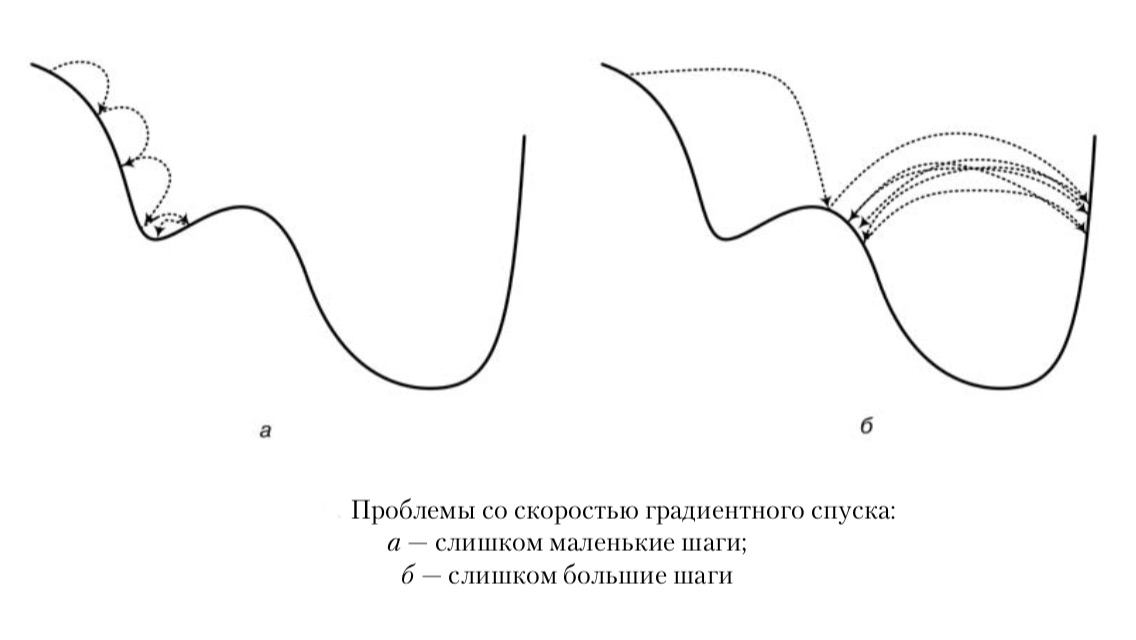
Для разумного сочетания быстроты и точности предлагается чередовать грубый и точный поиск в зависимости от того, насколько далеко мы находимся в данный момент \(x^i\). Зададим две константы \(\delta_1 < \delta_2\) и введём условия:
-
если \(\epsilon > \delta_2\), то увеличиваем \(h\)
-
если \(\delta_1 \le \epsilon < \delta_2\), то уменьшаем \(h\)
-
если \(\epsilon < \delta_1\), то поиск окончен.
Первообразная, интеграл.
Теперь рассмотрим обратную задачу: у нас есть функция \(f(x)\) (график или формула), которая является производной какой-то функции \(F(x)\). Вопрос:как найти эту функцию \(F(x)\)?
Из определения производной можем найти только разность двух состояний:
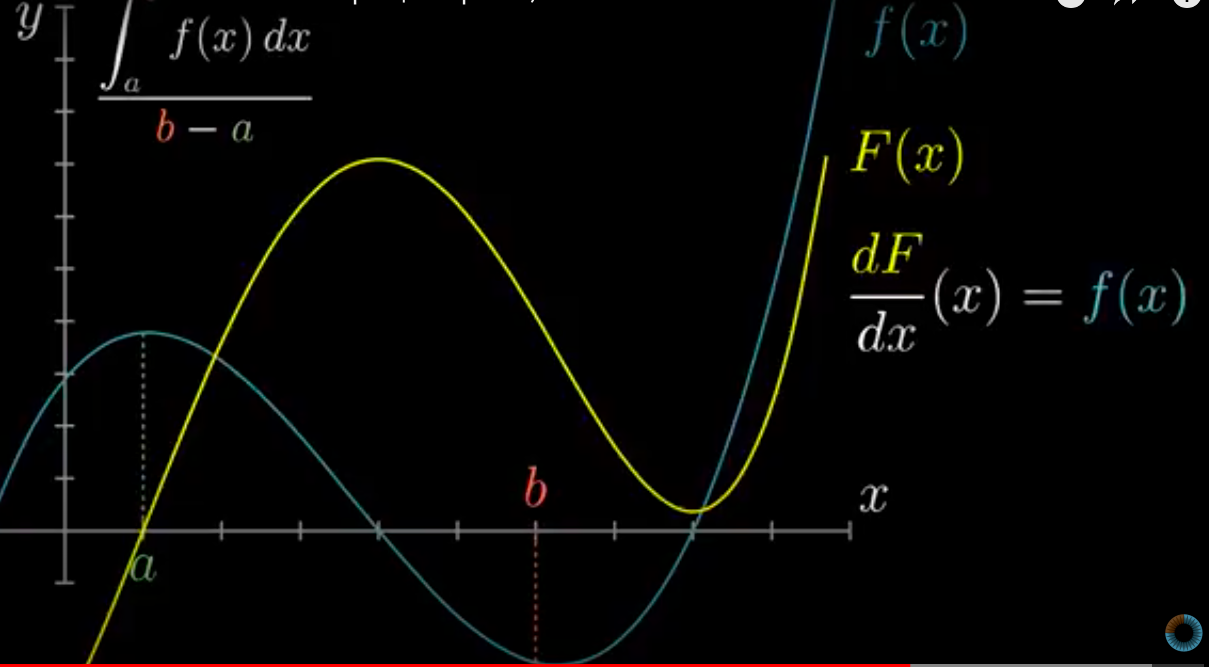
Попробуем интерпретировать задачу в терминах физики: получается, у нас есть скорость \(V(t)\), которая является изменением координаты точки на заданном участке пути. Но как всегда есть нюанс: мы знаем только скорость, но эта скорость может быть на любом участке пути, с одной и той же скоростью мы можем ехать по трассе Москва-Санкт-Петербург или Воронеж-Сочи. То есть сама координата нам не даст никакой информации, так как мы не знаем начало системы отсчёта (напоминает принцип Неопределённости Гейзенберга). А вот разность двух состояний/координат покажет, путь какой длины мы проехали.
Ещё одна аналогия из физики: потенциал сам по себе не несёт существенной информации - это работа по перемещению из бесконечно удалённой точки в точку \(A\), а работу по перемещению заряда из точки \(A\) в точку \(B\) как раз представляет разность потенциалов \(\phi(B)-\phi(A)\).
Итого, первообразная \(F(x)\) - просто математически введённая функция, которая подгоняется как обратное действие к операции дифференцирования при помощи таблицы производных. Общей формулы для нахождения первообразных, аналогичной формуле для вычисления производной частного и произведения, не существует. Отметим, что такая функция определена с точностью до константы или представляет собой семейство параллельных функций: если \(F(x)\) - первообразная, то и \(F(x)+c\) - тоже первообразная, где \(c=const\).
Строгое определение: первообразной для функции \(f(x)\) называется такая функция \(F(x)\), определённая на \((a;b)\), что \(F'(x) = f(x)\) для любого \(x \in (a;b)\).
Вернёмся к задаче о нахождении пройденного пути через известную скорость. В физических терминах \(\frac{dS}{dt} = V, \, V dt = dS\), а вот тут мы как раз используем дифференциал - разбиваем весь путь на очень маленькие промежутки по времени, и на каждом из таких промежутков рассматриваем движение как равномерное - с одной и той же скоростью (приближение линейной функцией), на графике это как раз будет площадь прямоугольника со сторонами \(V\) и \(dt\).
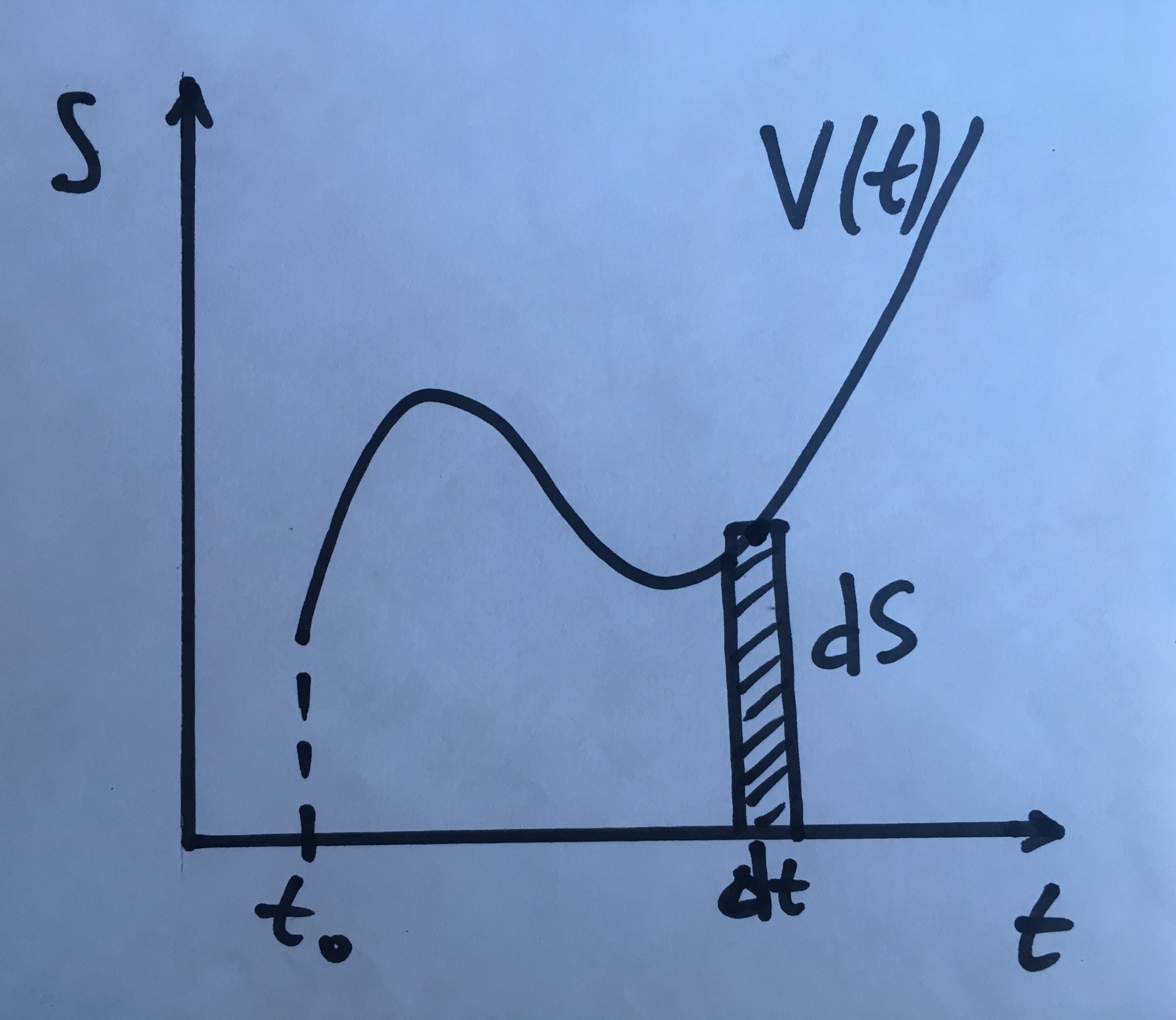
А весь пройденный путь как раз равен сумме таких кусочков: \(\quad S = \int_{t_1}^{t_2} V(t) \,dt\). А процесс суммирования в непрерывном случае назвали интегрированием. Отсюда получаем известный всем факт, что определённый интеграл равен площади под графиком функции.
Воспользуемся площадью как функцией: берём одну из первообразных \(F(x)= \int_{a}^{x} f(t)\,dt\) - зафиксировали начальную точку и движемся от неё вправо, получим функцию от конца пути или верхнего предела интегрирования, которая как раз покажет путь от \(a\) до \(x\). Отметим, что мы описали путь поиска первообразной и такое представление \(F(x)\) через интеграл - это пока наше предположение, надо математически доказать, что \(F'(x) = f(x)\) для любого \(x\).
Немного отвлечёмся на факт, который называется первая теорема о среднем, строгое доказательство можно найти в любом учебнике, нас интересует суть и физическая интерпретация:
Первая теорема о среднем. Пусть \(f(x)\) - непрерывная и ограниченная на \([a, b]\) функция, тогда на этом отрезке найдётся такая точка \(c\), что \(\int_{a}^{b} f(x)\,dx = f(c) \int_{a}^{b} dx = f(c) (b-a)\).
Пройденный путь можно найти как среднюю скорость \(f(c)\), умноженную на затраченное время \((b-a)\) - а это просто следует из физического определения средней скорости. Причём существует такой момент времени \(c\), в который величина скорости как раз равнялась средней - весьма понятный интуитивно факт.
Итак, строго математически докажем, что функция \(F(x)= \int_{a}^{x} f(t)\,dt\) будет первообразной для функции \(f(x)\):
\(F'(x_0) = \lim_{x \to x_0} \frac{F(x) - F(x_0)}{x-x_0} = \lim_{x \to x_0} { \frac{\int_{a}^{x} f(t)\,dt - \int_{a}^{x_0} f(t)\,dt}{x-x_0} } = \lim_{x \to x_0} {\frac{\int_{x_0}^{x} f(t)\,dt}{x-x_0} } = \lim_{x \to x_0} {\frac{f(c)(x-x_0)}{x-x_0} } = \lim_{x \to x_0} {f(c)} = f(x_0)\)
Последний переход обосновывается тем, что точка \(c\) лежит между \(x_0\) и \(x\), и при стремлении \(x \to x_0\) все три точки сжимаются в одну.
Преобразование Фурье. Вейвлет-преобразование. Оконные функции.
Исторически задача появилась, когда надо было понять характер поведения закреплённой колеблющейся струны. Возникает проблема: как описать более сложные формы, можно ли более сложные формы представить как сумму простейших, в нашем случае - синусоидальных кривых.
Период - это длина \(T\) промежутка времени, через которое наша функция \(f(x)\) начинает принимать те же значения: \(f(x − T) = f(x) = f(x + T)\).
Частота - количество повторений в единицу времени. В нашем случае под частотой будем понимать \(\omega = \frac{2\pi}{T}\).
Фаза - это «сдвиг функции» от нулевого значения, или координата пересечения оси \(x\) с графиком функции: \(\phi = \omega t + \phi\).
Амплитуда - длина максимального смещения вдоль оси \(y\) от среднего положения.
Первое представление разложения функции \(f(x)\) в ряд Фурье:
\(f(t) = \sum\limits_{k=0}^{\infty}\Big(a_k cos(k\omega t) + b_k sin(k\omega t)\Big)\)
\(a_k = \frac{2}{T}\int\limits_0^T f(t)cos(k \omega t)dt \;\;\;\; b_k = \frac{2}{T}\int\limits_0^T f(t)sin(k \omega t) dt\)
Второе представление разложения функции \(f(x)\) в ряд Фурье(просто преобразуем некоторым образом коэффициенты из первого разложения):
\(f(t) = \sum\limits_{k=0}^{\infty} A_k cos(k \omega t - \phi_k)\)
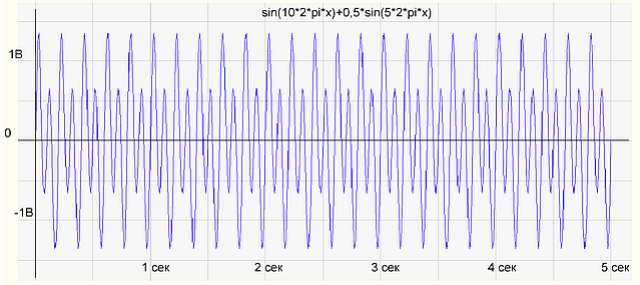
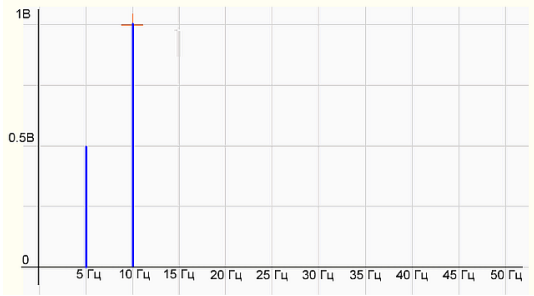
Здесь \(A_k = \sqrt{a_k^2 + b_k^2}\) - амплитуда, \(\phi_k = arctg \frac{b_k}{a_k}\) - фаза. Множество амплитуд \(\{A_k\}\) называется спектром сигнала и показывает распределение энергии сигнала по частотам. Это представление даёт возможность построить график зависимости амплитуды сигнала от частоты. На примере разложения мелодии по нотам частота - это ноты или те клавиши, на которые мы нажимаем, а амплитуда - сила, с которой мы нажимаем на каждую клавишу.
| |
|
|:--:|
|График амплитуды в зависимости от времени|
| |
|
|:--:|
|Спектр волны|
Пойдём дальше и вспомним формулу Эйлера - представление экспоненты через синус и косинус: \(e^{i \alpha} = cos \alpha + i sin\alpha\)
\(e^{ik \omega t} = cos(k \omega t) + isin(k \omega t) \;\;\; e^{−ik \omega t} = cos(k \omega t) − isin(k \omega t)\)
Третье представление разложения \(f(x)\) в ряд Фурье:
\(f(x) = \sum\limits_{-\infty}^{\infty} c_k e^{ik \omega t}\)
Всё, что мы делали ранее, относилось к периодическим функциям. Для непериодических функций логично совершить предельный переход
\(T \rightarrow \infty\) или \(\omega \rightarrow 0\), тогда параметр \(k\)
теряет смысл, и разумнее перейти к новой частоте \(\omega_1 = k\omega\):
\(F(w_1) = \int\limits_{-\infty}^{\infty} f(t) e^{-i w_1 t} dt\)
На практике нельзя получить сигнал на бесконечном интервале, так как нет возможности узнать, какой был сигнал до включения устройства и какой он будет в будущем. Для моделирования сигнала как в реальной жизни ограничим интервала анализа, что равносильно произведению исходного сигнала на оконную функцию. Таким образом, результатом оконного преобразования Фурье является не спектр исходного сигнала, а спектр произведения сигнала и оконной функции.
Оконная функция - это математическая функция, которая имеет нулевое значение за пределами некоторого выбранного интервала, обычно симметричная вокруг середины интервала, близкая к максимуму в середине и сужающаяся от середины.
Оконное преобразование Фурье - это разновидность преобразования Фурье, определяемая следующим образом:
\(F(t,\omega )=\int \limits_{-\infty }^{\infty }f(\tau)W(\tau -t)e^{-i\omega \tau}d\tau\)
где \(W(\tau - t)\) - некоторая оконная функция. В случае дискретного преобразования оконная функция используется аналогично:
\(F(m,\omega) = \sum\limits_{-\infty}^\infty f[n] w[n-m] e^{-i\omega n}d\tau\)
Ещё один выход для избежания проблем, возникающих при преобразовании Фурье - вместо разложения по синусам и косинусам взять другие системы ортогональных функций, самые известные: вейвлет "Хаара" и вейвлет "Мексиканская шляпа".
Вейвлет-преобразование - это его представление в виде обобщенного ряда или интеграла Фурье по системе базисных функций. Вейвлет-преобразование переводит сигнал из временного представления в частотно-временное. Это способ преобразования функции (или сигнала) в форму, которая или делает некоторые величины исходного сигнала более поддающимися изучению, или позволяет сжать исходный набор данных.
Польза Вейвлет-преобразования заключается в том, что в заданном сигнале мы можем находить функции, похожие на вейвлеты: если при заданном масштабе и сдвига получаем большое значение вейвлета, то в заданном сигнале будет похожий участок.
В отличие от преобразования Фурье вейвлет-преобразование дает двумерную развертку одномерного процесса, при этом частота и время рассматриваются как независимые переменные. В результате появляется возможность анализировать свойства процесса одновременно во временной и частотной областях.