Архитектуры нейронных сетей

Свёрточные нейронные сети. Семейства архитектур: LeNet, AlexNet, VGG, Inception, ResNet, DenseNet, EfficientNet.

LeNet

Первая современная сверточная сеть была придумана в 1989 году Яном Лекуном и сотечает в себе все необходимые вещи, используемые и по сей день:

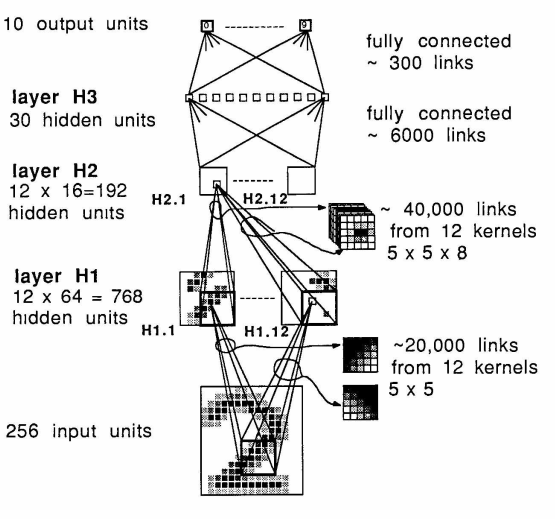
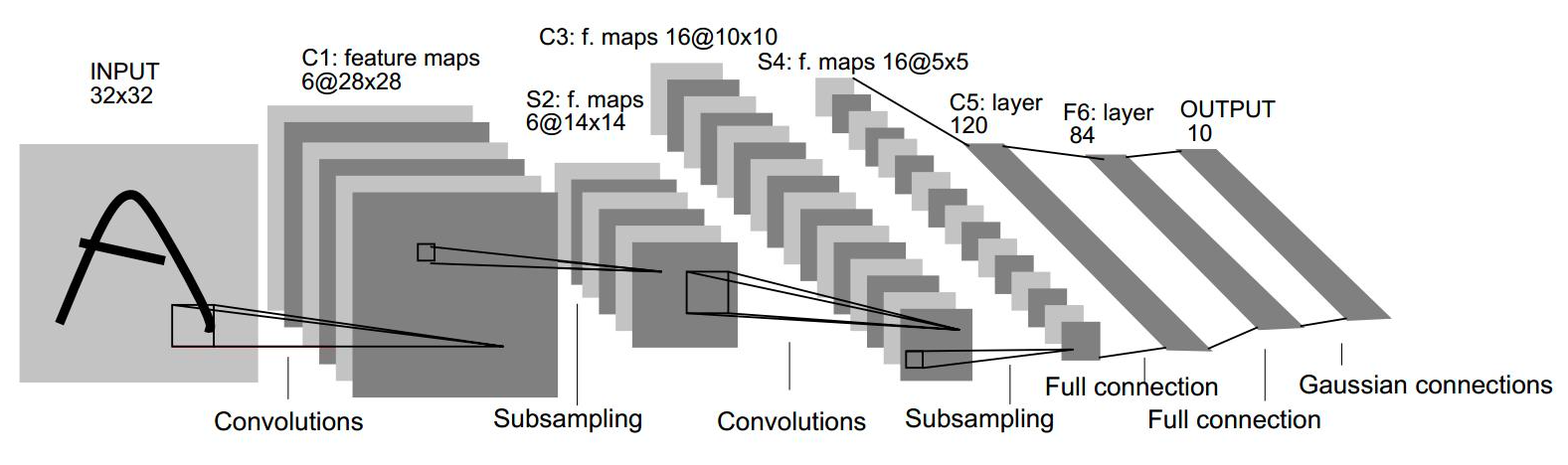
Первой известной сетью стала т.н. LeNet-5 от того же Лекуна. Изменения по сравнению с версией 1989 года:

• Появилось два слоя

• Постобработка на выходе (алгоритм Витерби и т.п.)

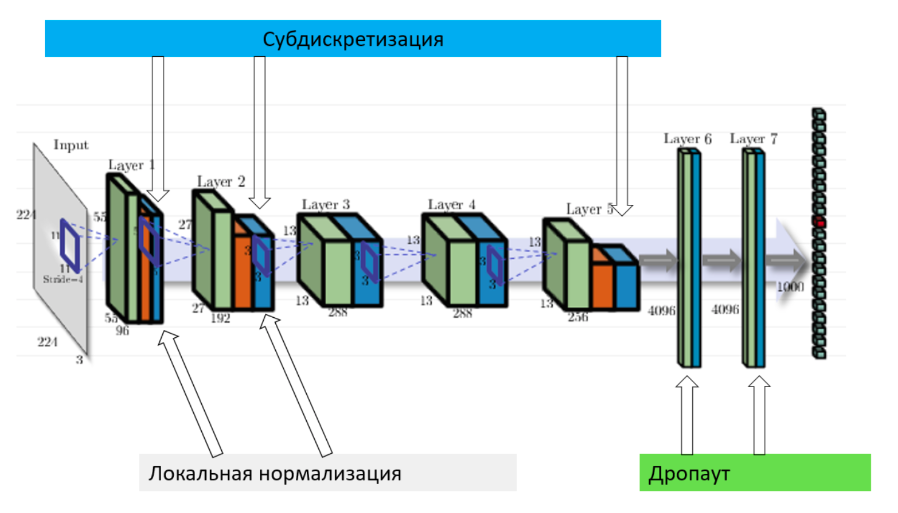
AlexNet

Именно AlexNet прославил СНС и положил начало их повсеместному использованию в компьютерном зрении. ПО сравнению с LeNet, привнес множество новых трюков.\ Особенности AlexNet

• Использование ReLU вместо sigmoid. Оказывается, если отказаться от классических на тот момент (2012) функций активации (simoid, tanh), то можно ускорить обучение СНС на порядок.

• Локальная нормализация активаций. Нормализуются карты активаций.

• Субдискретизация с перекрытием. Обычно субдискретизация (пулинг) используется с окном размера \(z=n\) и сдвигом (страйдом), равным размеру окна, т.е. \(s=n\). Однако, в AlexNet применяется пулинг с перекрытием в одну клетку, т.е. \(z=n, s=n-1\).

• обучающей выборки

• для уменьшения переобучения. Использовалось значение \(p=0.5\) на полносвязных слоях, на сверточных дропаут обычно не используется. Он помог с переобучением, но при этом время обучения возросло в \(\frac{1}{p}=2\) раза.

• Аугментация на тесте

Инициализация и оптимизатор

• Веса сверток задаются случайными числами из нормального распределения с нулевым средним и среднеквадратичным отклонением \(0.01\)

• Коэффициент сдвига в некоторых слоя инициализируется нулем, в некоторых (напр. полносвязных) - единицей

• Динамическое управление коэффициентом скорости обучения: коэффициент делится на 10, когда качество перестает улучшаться на валидационной выборке

• Оптимизатор - momentum (накопление градиента)

• \(L_2\)-регуляризация веса (weight decay)

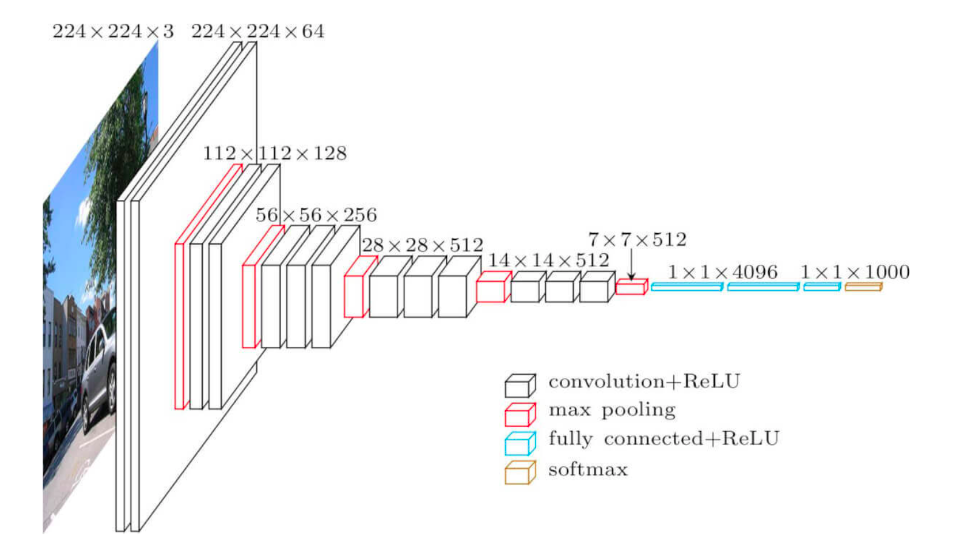
VGG

• Предложена в Visual Geometry Group (университет Оксфорда).

• Идея простой и глубокой сверточной сети доведена до макисмума.

  • Существуют 2 версии: VGG-16 и VGG-19 (по числу слоев с обучаемыми весами)

  • Содержит огромное число параметров (138 млн и 144 млн), дальнейшее увеличение глубины и параметров не дало прироста на ImageNet

• Используются только стандартные свертки размера \(3\times 3\) (к примеру, в AlexNet первые две свертки были размеров \(11\times 11\) и \(5\times 5\) )

• Входной размер \(224\times 224\)

Inception

Мотивация - хочется сделать глубокую НС, но простое добавление слоев, как в VGG не дает прироста в качестве.\ Особенности:

• Разреженная архитектура.

  • Проблема: линейное наращивание сверточных слоев достаточно быстро себя исчерпывает (вспомним VGG).

  • Идея: использование нелинейной разреженной архитектуры

• Конкатенация фильтров

  • Проблема: при линейной структуре у нас признаки с рецептивного поля (область, которая участвует в вычислении данного нейрона) одного размера (ограниченного размером свертки)

  • Идея: конкатенировать выходы сверток разного размера на слоях одной глубины

• Уменьшение сложности

  • Проблема: при большом количестве карт много вычислений свертки

  • Идея: с помощью свертки \(1\times 1\) предварительно уменьшить количество карт

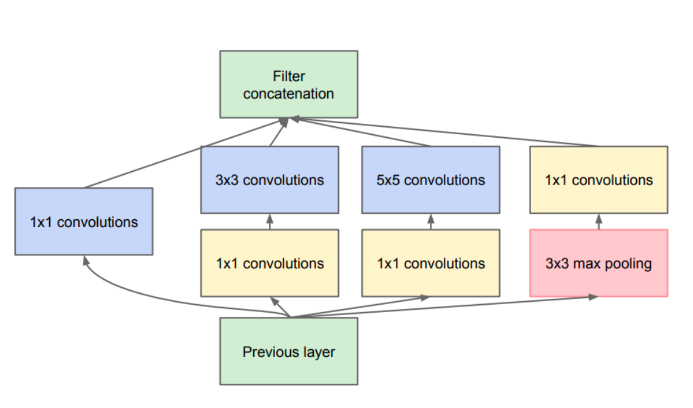
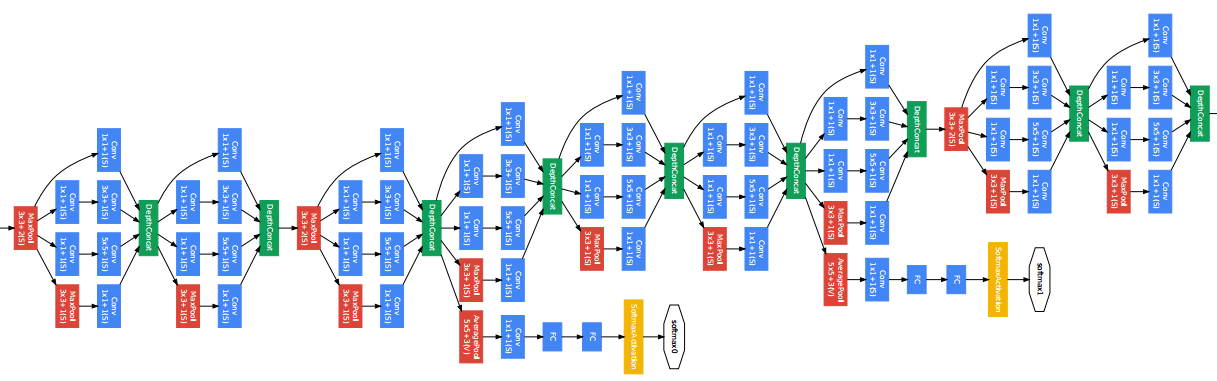
Сеть Inception состоит из множества Inception-блоков.

Inception. Детали архитектуры.

• Количество составных блоков около 100

• Глубина 27 слоев, из них 22 - с обучаемыми параметрами

• Перед последним полносвязным слоем - GAP

• Введены два дополнительных классификатора в середине сети (борьба с затухающим градиентом, регуляризация)

• Функции потерь для дополнительных классификаторов домножаются на \(0.3\)

• Используется дропаут

ResNet

При увеличении "плоских" слоев в стиле VGG качество сети падает, а не растет (даже на обучающей выборке, не говоря уже о тестовой). При большой глубине НС возникает проблема затухающего градиента, таким образом, сеть перестает обучаться.

Будем вместо целевой функции \(H(x)\) обучать остаточную (residual\(\Rightarrow\) ResNet) функцию \(F(x)=H(x)-x\), а целевую рассчитывать как поточечную сумму входа \(x\) и остаточной функции \(F(x): H(x)=F(x)+x\).

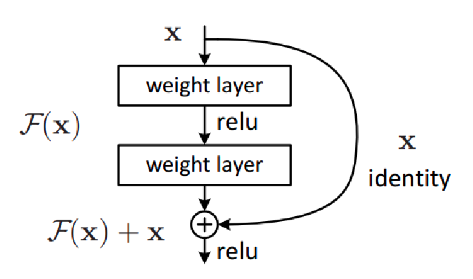
Таким образом мы дополнительно прокидываем тождественные связи (identity) между входом и выходом остаточной функции (боремся с затухающим градиентом). Эти тождественные связи носят название "skip-connections" или "short-cuts".

• Наиболее известны следующие разновидности ResNet (по числу сверточных слоев): ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152

• Для более глубоких сетей используется большее число карт признаков \(\Rightarrow\) многократно возрастает количество весов фильтров и число операций

• Авторы предлагают использовать дизайн бутылочного горлышка (bottleneck) - сначала уменьшить кол-во карт с помощью сверток \(1\times 1\), затем применить обычную свертку \(3\times 3\), и, наконец, вернуть кол-во карт свертками \(1\times 1\). (Отчасти процедура схожая с такой же в Inception)

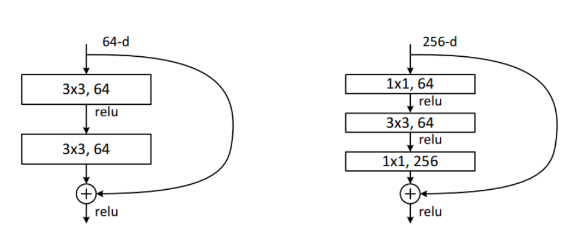
Архитектурные особенности

• Перед последним полносвязным слоем применяется GAP (Global Average Pooling)

• Принцип сохранения сложности (уменьшаем пространственный размер в 2 раза \(\Rightarrow\) одновременно увеличиваем в 2 раза кол-во карт признаков)

• Почти везде уменьшение размерности через свертки с шагом (stride) = 2

• BatchNorm используется после каждой свертки

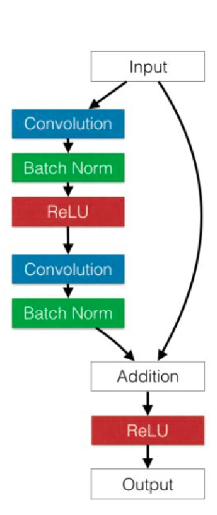
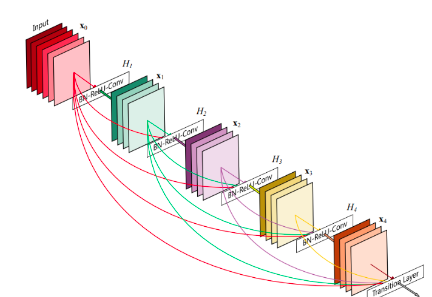
DenseNet

Нужно больше соединений!

• Было предложено в рамках слоев одинакового пространственного разрешения использовать вообще все возможные связи с помощью конкатенции.

• Таким образом, если слоев \(L\), то таких связей будет \(L(L-1)/2\)

• DenseNet выигрывает у ResNet

EfficientNet

Основная информация: сеть подбирается автоматически (с помощью специального фремворка) по сетке параметров. Нужна быстрая и легкая сеть\ Проблема: нужно оптимизировать сверточную нейронную сеть. Предыдущие методы произвольно масштабировали размерность нейросети (например, количество слоев и параметров). Предложенный метод равномерно масштабирует части нейросети с фиксированными коэффициентами масштабирования. Оптимизированные сети (EfficientNets) обходят state-of-the-art подходы по точности при увеличении эффективности в 10 раз (меньше и быстрее).\ Эффективность масштабирования нейросети зависит от ее начальной архитектуры. Чтобы улучшить работу нейросети, исследователи выбирали начальную архитектуру автоматически с помощью AutoML фреймворка --- MNAS. MNAS при выборе устройства нейросети оптимизирует и точность модели, и ее размер одновременно. В итоге начальная модель использовала архитектуру MBConv, схожую с MobileNetV2 и MnasNet. Начальная модель затем масштабировалась и породила класс EfficientNets моделей.

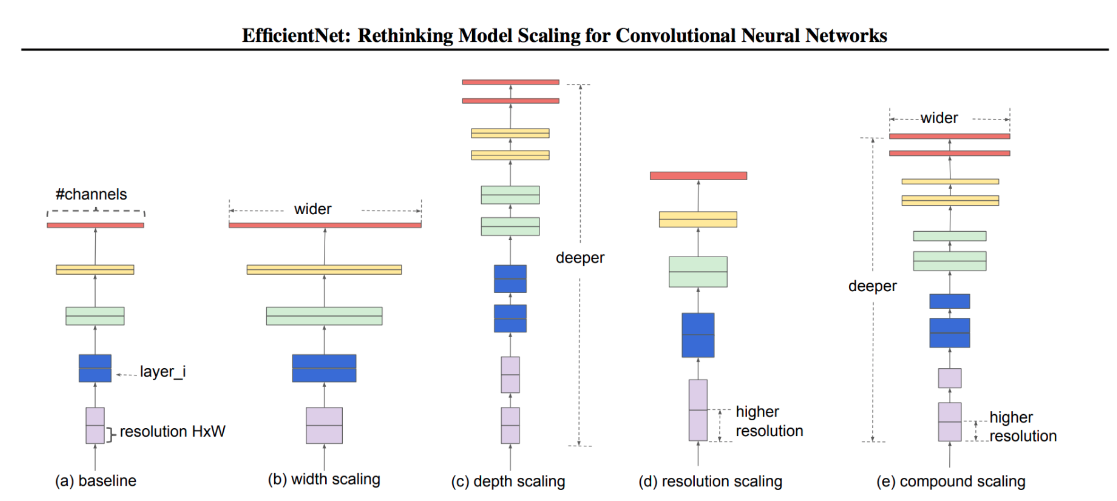
Оптимизируются следующие параметры:

• Глубина: \(d=\alpha^{\Phi}\)

• Ширина: \(w=\beta^{\Phi}\)

• Разрешение (resolution): \(r=\gamma^{\Phi}\)

• s.t. \(\alpha\cdot\beta^{2}\cdot\gamma^{2}\approx 2, \alpha\geq 1, \beta\geq 1, \gamma\geq 1\) - должно соблюдаться соотношение, выведенное эмпирическим путем (обоснования нет)

Шаги:

• Шаг 1: для \(\Phi=1.0\) параметры подбираются перебором по сетке: \(\alpha=1.2, \beta=1.1, \gamma=1.15\)

• Шаг 2: При фиксированных \(\alpha=1.2, \beta=1.1, \gamma=1.15\), меняя \(\Phi\) получаем большие модели.

Контрастивное обучение. Примеры из компьютерного зрения и языковых задач. Сиамские сети. Функции потерь: constrastive loss, triplet loss.

Сиамская сеть

В московском метро есть системы для распознавания лиц. Людей в Москве огромное количество, поэтому нейронные сети не решают задачу классификации, иначе output вектор был бы огромной размерности, и меток при обучении тоже будет очень много. Тем не менее иногда хочется разыскивать людей или еще что. Мы можем сравнивать людей с фотографиями в базе. Необходимо уметь отвечать на вопрос -- являются ли эти два изображения представителями одного класса?.

Сиамская сеть -- это сеть, в которой два раза дублируется одна и та же архитектура, причём веса у них общие. Входные экземпляры подаются по одному в каждую сеть (например, две картинки). В результате получаем два вектора embedding, которые и можно сравнить на схожесть с помощью constrative loss.

При обучении такой сети можно аугментировать фото одного и того же человека и ожидать на выходе метку 1 -- фото одного человека. И ожидать метку 0 для фотографий разных людей.

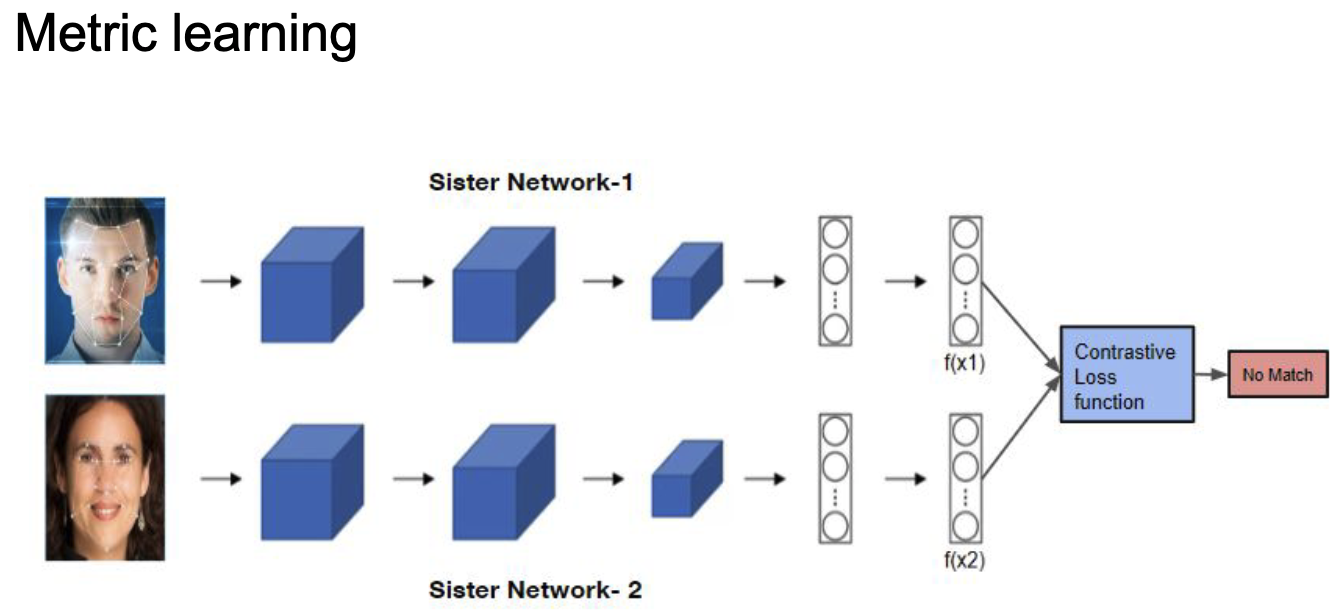Сиамская нейронная сеть.

Constrastive loss

Для каждого фиксированного изображения -- якоря (anchor) мы можем сопоставить изображение того же класса (positive) и изображение из другого класса (negative). Тогда эталонный ответ в первом случае должен быть 1, а во втором 0. (\(r\) -- embedding, \(d\) -- расстояние, \(margin\) -- некоторая константа, на которое хотим отделить негативные пары)

Constrastive loss для сиамской сети:

\[L = \begin{cases} d(r_{anchor}, r_{positive}), & \text{if positive pair}\\ max(0, margin - d(r_{anchor}, r_{negative})), & \text{if negative pair} \end{cases}\]

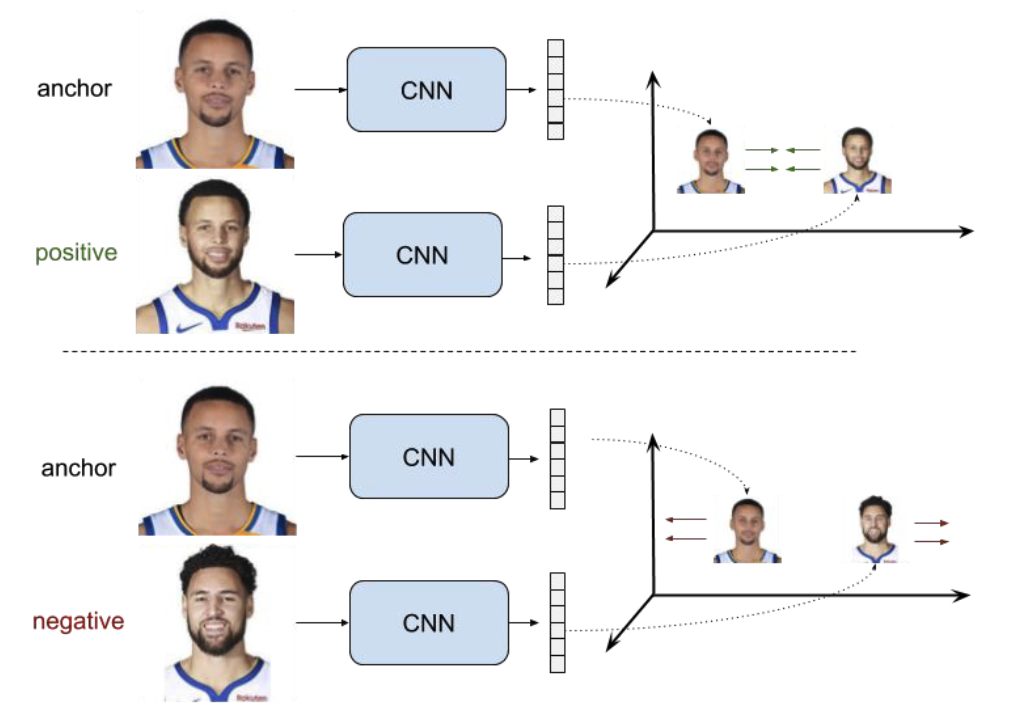Пример якоря, и изображений позитивного и негативного классов.

Triplet loss

Рассмотрим теперь аналог сиамской сети -- сеть, состоящую из трёх частей с общей архитектурой и одинаковыми весами, которая на вход принимает \(3\) изображения -- якорь, изображение позитивного класса и изображение негативного класса.

Для этой сети можно рассмотреть похожий по логике triplet loss:

\[L = max(0, margin + d(r_{anchor}, r_{positive}) - d(r_{anchor}, r_{negative})).\]

Теперь не сиамская сеть, а скажем "тройная"